
【题目】已知数列{an}满足0<an<1,且an+1+ ![]() =2an+
=2an+ ![]() (n∈N*).
(n∈N*).
(1)证明:an+1<an;
(2)若a1= ![]() ,设数列{an}的前n项和为Sn , 证明:
,设数列{an}的前n项和为Sn , 证明: ![]() ﹣
﹣ ![]() <Sn<
<Sn< ![]() ﹣2.
﹣2.
【答案】
(1)证明:由an+1+ ![]() =2an+
=2an+ ![]() ,
,
得 ![]() ,即
,即 ![]() ,
,
∴ ![]() ,则
,则 ![]() ,
,
又0<an<1,
∴ ![]() ,即an+1<an
,即an+1<an
(2)证明:由an+1+ ![]() =2an+
=2an+ ![]() ,得
,得 ![]() .
.
∴Sn=a1+a2+…+an= ![]() +…+
+…+ ![]()
= ![]() .
.
又∵an+1+ ![]() =2an+
=2an+ ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
由0<an+1<an,可知 ![]() ,
,
即 ![]() ,
,
∴2n ![]() ,
,
∴ ![]() ,
, ![]() ,
,
∵ ![]() .
.
∴ ![]() .
.
∴ ![]() ﹣
﹣ ![]() <Sn<
<Sn< ![]() ﹣2.
﹣2.
【解析】(1)把已知数列递推式变形,可得 ![]() ,结合0<an<1,得到an+1﹣an=
,结合0<an<1,得到an+1﹣an= ![]() <0,即an+1<an;(2)由已知数列递推式得
<0,即an+1<an;(2)由已知数列递推式得 ![]() ,利用累加法得到Sn=
,利用累加法得到Sn= ![]() =an+1+
=an+1+ ![]() .把已知递推式两边平方可得
.把已知递推式两边平方可得 ![]() ,利用放缩法得到
,利用放缩法得到 ![]() ,即2n
,即2n ![]() ,进一步得到
,进一步得到 ![]() ,然后利用不等式的可加性证得
,然后利用不等式的可加性证得 ![]() ﹣
﹣ ![]() <Sn<
<Sn< ![]() ﹣2.
﹣2.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系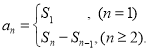 ).
).


科目:高中数学 来源: 题型:
【题目】已知抛物线关于![]() 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点![]() 在抛物线上.
在抛物线上.
(1)写出该抛物线的标准方程及其准线方程;
(2)过点![]() 作两条倾斜角互补的直线与抛物线分别交于不同的两点
作两条倾斜角互补的直线与抛物线分别交于不同的两点![]() ,求证:直线
,求证:直线![]() 的斜率是一个定值.
的斜率是一个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①对立事件一定是互斥事件;②若A,B为两个随机事件,则P(A∪B)=P(A)+P(B);③若事件A,B,C彼此互斥,则P(A)+P(B)+P(C)=1;④若事件A,B满足P(A)+P(B)=1,则A与B是对立事件.
其中正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,AB=2,cosB= ![]() ,点D在线段BC上.
,点D在线段BC上. 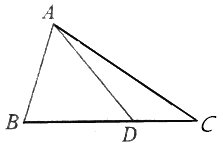
(1)若∠ADC= ![]() π,求AD的长;
π,求AD的长;
(2)若BD=2DC,△ACD的面积为 ![]()
![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:max{a,b}= ![]() ,若实数x,y满足:|x|≤3,|y|≤3,﹣4x≤y≤
,若实数x,y满足:|x|≤3,|y|≤3,﹣4x≤y≤ ![]() x,则max{|3x﹣y|,x+2y}的取值范围是( )
x,则max{|3x﹣y|,x+2y}的取值范围是( )
A.[ ![]() ,7]
,7]
B.[0,12]
C.[3, ![]() ]
]
D.[0,7]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点在原点
的顶点在原点![]() ,对称轴是
,对称轴是![]() 轴,且过点
轴,且过点![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知斜率为![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,且与曲线
,且与曲线![]() 相切于点
相切于点![]() ,点
,点![]() 在曲线
在曲线![]() 上,且直线
上,且直线![]() 轴,
轴, ![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,判断点
,判断点![]() 是否共线,并说明理由.
是否共线,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com