
【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,AA1=AD=1,E为CD的中点. 
(1)求证:B1E⊥AD1
(2)若二面角A﹣B1E﹣A1的大小为30°,求AB的长.
【答案】
(1)证明:(以A为原点, ![]() ,
, ![]() ,
, ![]() 的方向分别为x轴,y轴,z轴的正方向,
的方向分别为x轴,y轴,z轴的正方向,
建立如图所示的空间直角坐标系.
设AB=a,则A(0,0,0),D(0,1,0),D1(0,1,1),E( ![]() ,1,0),B1(a,0,1),
,1,0),B1(a,0,1),
![]() =(a,0,1),
=(a,0,1), ![]() =(
=( ![]() ,1,0),
,1,0), ![]() =(0,1,1),
=(0,1,1), ![]() =(﹣
=(﹣ ![]() ,1,﹣1)
,1,﹣1)
∵ ![]() =﹣
=﹣ ![]() ×0+1×1+(﹣1)×1=0,
×0+1×1+(﹣1)×1=0,
∴B1E⊥AD1.

(2)解:连结A1D,B1C,由长方体ABCDA1B1C1D1及AA1=AD=1,得AD1⊥A1D.
∵B1C∥A1D,∴AD1⊥B1C.
又由(1)知B1E⊥AD1,且B1C∩B1E=B1,
∴AD1⊥平面DCB1A1,
∴ ![]() =(0,1,1)是平面A1B1E的一个法向量,
=(0,1,1)是平面A1B1E的一个法向量,
设平面AB1E的法向量 ![]() =(x,y,z),
=(x,y,z),
则  ,取x=1,得
,取x=1,得 ![]() =(1,﹣
=(1,﹣ ![]() ,﹣a),
,﹣a),
∵二面角AB1EA1的大小为30°,
∴|cos< ![]() >|=cos 30°,即
>|=cos 30°,即  =
=  =
= ![]() ,
,
解得a=2,即AB的长为2.
【解析】(1)以A为原点, ![]() ,
, ![]() ,
, ![]() 的方向分别为x轴,y轴,z轴的正方向,建立空间直角坐标系,利用向量法能证明B1E⊥AD1 . (2)求出平面A1B1E的一个法向量和平面AB1E的法向量,由二面角A﹣B1E﹣A1的大小为30°,利用向量法能求出AB的长
的方向分别为x轴,y轴,z轴的正方向,建立空间直角坐标系,利用向量法能证明B1E⊥AD1 . (2)求出平面A1B1E的一个法向量和平面AB1E的法向量,由二面角A﹣B1E﹣A1的大小为30°,利用向量法能求出AB的长


科目:高中数学 来源: 题型:
【题目】椭圆的中心在原点O,短轴长为 ![]() ,左焦点为F(﹣c,0)(c>0),直线
,左焦点为F(﹣c,0)(c>0),直线 ![]() 与x轴交于点A,且
与x轴交于点A,且 ![]() ,过点A的直线与椭圆相交于P,Q两点.
,过点A的直线与椭圆相交于P,Q两点. 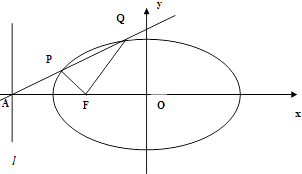
(1)求椭圆的方程.
(2)若 ![]() ,求直线PQ的方程.
,求直线PQ的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=2sin(2x+ ![]() ),g(x)=mcos(2x﹣
),g(x)=mcos(2x﹣ ![]() )﹣2m+3(m>0),若对任意x1∈[0,
)﹣2m+3(m>0),若对任意x1∈[0, ![]() ],存在x2∈[0,
],存在x2∈[0, ![]() ],使得g(x1)=f(x2)成立,则实数m的取值范围是( )
],使得g(x1)=f(x2)成立,则实数m的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)定义域为[0,+∞),当x∈[0,1]时,f(x)=sinπx,当x∈[n,n+1]时,f(x)= ![]() ,其中n∈N,若函数f(x)的图象与直线y=b有且仅有2016个交点,则b的取值范围是( )
,其中n∈N,若函数f(x)的图象与直线y=b有且仅有2016个交点,则b的取值范围是( )
A.(0,1)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据调查分析,若干年内某产品关税与市场供应量P的关系近似地满足:y=P(x)=2 ![]() ,(其中,t为关税的税率,且t∈[0,
,(其中,t为关税的税率,且t∈[0, ![]() ),x为市场价格,b,k为正常数),当t=
),x为市场价格,b,k为正常数),当t= ![]() 时的市场供应量曲线如图.
时的市场供应量曲线如图. 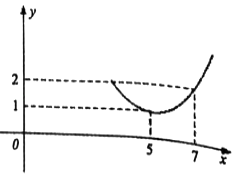
(Ⅰ)根据图象求b,k的值;
(Ⅱ)若市场需求量为Q(x)=2 ![]() ,当p=Q时的市场价格称为市场平衡价格,当市场平衡价格保持在10元时,求税率t的值.
,当p=Q时的市场价格称为市场平衡价格,当市场平衡价格保持在10元时,求税率t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,且∠BAD=60°,A1A=AB,E为BB1延长线上的一点,D1E⊥面D1AC.设AB=2. 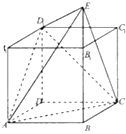
(1)求二面角E﹣AC﹣D1的大小;
(2)在D1E上是否存在一点P,使A1P∥面EAC?若存在,求D1P:PE的值;不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com