
【题目】椭圆的中心在原点O,短轴长为 ![]() ,左焦点为F(﹣c,0)(c>0),直线
,左焦点为F(﹣c,0)(c>0),直线 ![]() 与x轴交于点A,且
与x轴交于点A,且 ![]() ,过点A的直线与椭圆相交于P,Q两点.
,过点A的直线与椭圆相交于P,Q两点. 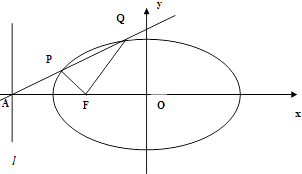
(1)求椭圆的方程.
(2)若 ![]() ,求直线PQ的方程.
,求直线PQ的方程.
【答案】
(1)解:设 ![]() ,
,
则 ![]() ,
, ![]() ,
,
解得a2=4,c=1,
所以椭圆方程为 ![]() .
.
(2)解:设PQ的方程为y=k(x+4),P(x1,y1),Q(x2,y2),F(﹣1,0)
∵PF⊥QF,∴(x1+1)(x2+1)+y1y2=0,
即 ![]() ,
, ![]() .
.
联立得 ![]()
消去y,得(3+4k2)x2+32k2x+64k2﹣12=0,
由△>0,得 ![]() .
.
∴ ![]() .
.
代入(*)式化简,得8k2=1,∴ ![]() .
.
则直线PQ的方程为 ![]() .
.
【解析】(1)设 ![]() ,由题意可得
,由题意可得 ![]() ,
, ![]() ,c2=a2+b2 , 解出即可;(2)设PQ的方程为y=k(x+4),P(x1 , y1),Q(x2 , y2),F(﹣1,0),把方程与椭圆方程联立得到根与系数的关系,再利用
,c2=a2+b2 , 解出即可;(2)设PQ的方程为y=k(x+4),P(x1 , y1),Q(x2 , y2),F(﹣1,0),把方程与椭圆方程联立得到根与系数的关系,再利用 ![]()
![]() 即可得出.
即可得出.
【考点精析】关于本题考查的椭圆的标准方程,需要了解椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能得出正确答案.
才能得出正确答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】将函数f(x)=sinωx(ω>0)的图象向右平移 ![]() 个单位后得到函数g(x)的图象,若对于满足|f(x1)﹣g(x2)|=2的x1 , x2 , 有|x1﹣x2|min=
个单位后得到函数g(x)的图象,若对于满足|f(x1)﹣g(x2)|=2的x1 , x2 , 有|x1﹣x2|min= ![]() ,则f(
,则f( ![]() )的值为 .
)的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点. 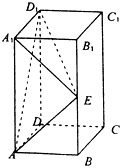
(1)求证:直线AE⊥平面A1D1E;
(2)求二面角E﹣AD1﹣A1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F(0,1),点P在x轴上,点Q在y轴上, ![]() =2
=2 ![]() ,
, ![]() ⊥
⊥ ![]() ,当点P在x轴上运动时,点N的轨迹为曲线C.
,当点P在x轴上运动时,点N的轨迹为曲线C.
(1)求曲线C的方程;
(2)过点F的直线l交曲线C于A,B两点,且曲线C在A,B两点处的切线相交于点M,若△MAB的三边成等差数列,求此时点M到直线AB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an},公差为2,的前n项和为Sn , 且a1 , S2 , S4成等比数列,
(1)求数列{an}的通项公式;
(2)设bn= ![]() (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,AA1=AD=1,E为CD的中点. 
(1)求证:B1E⊥AD1
(2)若二面角A﹣B1E﹣A1的大小为30°,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com