
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足:
满足:
对于任意![]() ,都有
,都有![]() 成立.
成立.
①求数列![]() 的通项公式;
的通项公式;
②设数列![]() ,问:数列
,问:数列![]() 中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() .(2)①
.(2)①![]() ,
,![]() .②见解析.
.②见解析.
【解析】分析:(1)当![]() 时,类比写出
时,类比写出![]() ,两式相减整理得
,两式相减整理得![]() ,当
,当![]() 时,求得
时,求得![]() ,从而求得数列
,从而求得数列![]() 的通项公式.;
的通项公式.;
(2)①将![]() 代入已知条件,用与(1)相似的方法,变换求出数列
代入已知条件,用与(1)相似的方法,变换求出数列![]() 的通项公式;
的通项公式;
②由![]() 的通项公式分析,得
的通项公式分析,得![]() …,假设存在三项
…,假设存在三项![]() ,
,![]() ,
,![]() 成等差数列,且
成等差数列,且![]() ,则
,则![]() ,即
,即![]() ,根据数列
,根据数列![]() 的单调性,化简得
的单调性,化简得![]() ,将
,将![]() 或
或![]() 代入已知条件,即可得到结论.
代入已知条件,即可得到结论.
详解:解:(1)由![]() , ①
, ①
得![]() , ②
, ②
由①-②得![]() ,即
,即
对①取![]() 得,
得,![]() ,所以
,所以![]() ,所以
,所以![]() 为常数,
为常数,
所以![]() 为等比数列,首项为1,公比为
为等比数列,首项为1,公比为![]() ,即
,即![]() ,
,![]() .
.
(2)①由![]() ,可得对于任意
,可得对于任意![]() 有
有
![]() , ③
, ③
则![]() , ④
, ④
则![]() , ⑤
, ⑤
由③-⑤得![]() ,
,
对③取![]() 得,
得,![]() 也适合上式,
也适合上式,
因此![]() ,
,![]() .
.
②由(1)(2)可知![]() ,
,
则![]() ,
,
所以当![]() 时,
时,![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 且
且![]() 上单调递减,
上单调递减,
故![]() …,
…,
假设存在三项![]() ,
,![]() ,
,![]() 成等差数列,其中
成等差数列,其中![]() ,
,![]() ,
,![]() ,
,
由于![]() …,可不妨设
…,可不妨设![]() ,则
,则![]() (*),
(*),
即![]() ,
,
因为![]() ,
,![]() ,
,![]() 且
且![]() ,则
,则![]() 且
且![]() ,
,
由数列![]() 的单调性可知,
的单调性可知,![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() ,
,
即![]() ,化简得
,化简得![]() ,
,
又![]() 且
且![]() ,所以
,所以![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,由
,由![]() 时,
时,![]() ,此时
,此时![]() ,
,![]() ,
,![]() 不构成等差数列,不合题意,
不构成等差数列,不合题意,
当![]() 时,由题意
时,由题意![]() 或
或![]() ,即
,即![]() ,又
,又![]() ,代入(*)式得
,代入(*)式得![]() ,
,
因为数列![]() 在
在![]() 且
且![]() 上单调递减,且
上单调递减,且![]() ,
,![]() ,所以
,所以![]() ,
,
综上所述,数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() 或
或![]() ,
,![]() ,
,![]() 构成等差数列.
构成等差数列.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的3个红球和3个黑球,现从甲、乙两个盒内各任取2个球。
(1)求取出的4个球中没有红球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设![]() 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
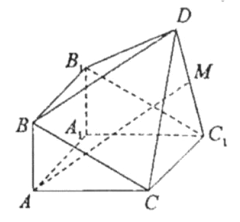
【题目】如图,由直三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中,![]() ,平面
,平面![]() 平面
平面![]()
(I)求证:![]() ;
;
(II)若M为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(III)在线段BC上(含端点)是否存在点P,使直线DP与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 得值,若不存在,说明理由.
得值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,(
,(![]() ).
).
(1)若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求实数am的值;
,求实数am的值;
(2)关于x的方程![]() 能否有三个不同的实根?证明你的结论;
能否有三个不同的实根?证明你的结论;
(3)若![]() 对任意
对任意![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
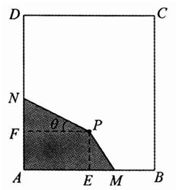
【题目】(题文)如图,长方形材料![]() 中,已知
中,已知![]() ,
,![]() .点
.点![]() 为材料
为材料![]() 内部一点,
内部一点,![]() 于
于![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,![]() . 现要在长方形材料
. 现要在长方形材料![]() 中裁剪出四边形材料
中裁剪出四边形材料![]() ,满足
,满足![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() ,
,![]() 上.
上.
(1)设![]() ,试将四边形材料
,试将四边形材料![]() 的面积表示为
的面积表示为![]() 的函数,并指明
的函数,并指明![]() 的取值范围;
的取值范围;
(2)试确定点![]() 在
在![]() 上的位置,使得四边形材料
上的位置,使得四边形材料![]() 的面积
的面积![]() 最小,并求出其最小值.
最小,并求出其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某超市2018年12个月的收入与支出数据的折线图如图所示:
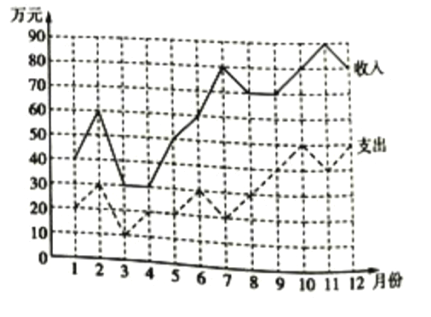
根据该折线图可知,下列说法错误的是( )
A. 该超市2018年的12个月中的7月份的收益最高
B. 该超市2018年的12个月中的4月份的收益最低
C. 该超市2018年1-6月份的总收益低于2018年7-12月份的总收益
D. 该超市2018年7-12月份的总收益比2018年1-6月份的总收益增长了90万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在学习强国活动中,某市图书馆的科技类图书和时政类图书是市民借阅的热门图书.为了丰富图书资源,现对已借阅了科技类图书的市民(以下简称为“问卷市民”)进行随机问卷调查,若不借阅时政类图书记1分,若借阅时政类图书记2分,每位市民选择是否借阅时政类图书的概率均为![]() ,市民之间选择意愿相互独立.
,市民之间选择意愿相互独立.
(1)从问卷市民中随机抽取4人,记总得分为随机变量![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)(i)若从问卷市民中随机抽取![]() 人,记总分恰为
人,记总分恰为![]() 分的概率为
分的概率为![]() ,求数列
,求数列![]() 的前10项和;
的前10项和;
(ⅱ)在对所有问卷市民进行随机问卷调查过程中,记已调查过的累计得分恰为![]() 分的概率为
分的概率为![]() (比如:
(比如:![]() 表示累计得分为1分的概率,
表示累计得分为1分的概率,![]() 表示累计得分为2分的概率,
表示累计得分为2分的概率,![]() ),试探求
),试探求![]() 与
与![]() 之间的关系,并求数列
之间的关系,并求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱 ABC﹣A1B1C1 中,AB 1 ,若二面角 C AB C1 的大小为 60°,则点 C 到平面 ABC1 的距离为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com