
【题目】
某园艺公司种植了一批名贵树苗,为了解树苗的生长情况,从这批树苗中随机地测量了![]() 棵树苗的高度(单位:厘米),并把这些高度列成如下的频数分布表:
棵树苗的高度(单位:厘米),并把这些高度列成如下的频数分布表:
组别 |
|
|
|
|
|
|
频数 | 2 | 4 | 11 | 16 | 13 | 4 |
(Ⅰ)在这批树苗中任取一棵,其高度在![]() 厘米以上的概率大约是多少?这批树苗的平均高度大约是多少?
厘米以上的概率大约是多少?这批树苗的平均高度大约是多少?
(Ⅱ)为了进一步获得研究资料,标记![]() 组中的树苗为
组中的树苗为![]() ,
,![]() 组中的树苗为
组中的树苗为![]() ,现从
,现从![]() 组中移出一棵树苗,从
组中移出一棵树苗,从![]() 组中移出两棵树苗进行试验研究,则
组中移出两棵树苗进行试验研究,则![]() 组的树苗
组的树苗![]() 和
和![]() 组的树苗
组的树苗![]() 同时被移出的概率是多少?
同时被移出的概率是多少?
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)根据题意,由频率分布表可得高度不低于80厘米的频数,进而由等可能事件的概率公式,计算可得答案;
(Ⅱ)设![]() 组中的树苗为
组中的树苗为![]() 组中的树苗为
组中的树苗为![]() 用列表法可得移出1棵树苗的基本事件的数目与
用列表法可得移出1棵树苗的基本事件的数目与![]() 同时被移出的事件数目,由等可能事件的概率公式计算可得答案.
同时被移出的事件数目,由等可能事件的概率公式计算可得答案.
试题解析:(Ⅰ)在这批树苗中任取一棵,其高度在![]() 厘米以上的概率大约是
厘米以上的概率大约是![]()
这批树苗的平均高度大约是
![]() (cm)
(cm)
(Ⅱ)从![]() 组中移出一棵树苗,从
组中移出一棵树苗,从![]() 组中移出两棵树苗的所有可能为ACD,ACE,ACF,ADE,ADF,AEF,BCD,BCE,BCF,BDE,BDF,BEF共12种,
组中移出两棵树苗的所有可能为ACD,ACE,ACF,ADE,ADF,AEF,BCD,BCE,BCF,BDE,BDF,BEF共12种,
其中![]() 组的树苗
组的树苗![]() 和
和![]() 组的树苗
组的树苗![]() 同时被移出的可能为ACD,ACE,ACF,共3种.
同时被移出的可能为ACD,ACE,ACF,共3种.
设![]() 组的树苗
组的树苗![]() 和
和![]() 组的树苗
组的树苗![]() 同时被移出为事件M,
同时被移出为事件M,
则![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】以下四个命题中:
①某地市高三理科学生有15000名,在一次调研测试中,数学成绩![]() 服从正态分布
服从正态分布![]() ,已知
,已知![]() ,若按成绩分层抽样的方式抽取100份试卷进行分析,则应从120分以上(包括120分)的试卷中抽取
,若按成绩分层抽样的方式抽取100份试卷进行分析,则应从120分以上(包括120分)的试卷中抽取![]() 份;
份;
②已知命题![]() ,则
,则![]() :
:![]() ;
;
③在![]() 上随机取一个数
上随机取一个数![]() ,能使函数
,能使函数![]() 在
在![]() 上有零点的概率为
上有零点的概率为![]() ;
;
④设![]() ,则“
,则“![]() ”是“
”是“![]() ”的充要条件.
”的充要条件.
其中真命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足a1=1,nan+1=(n+1)an+n(n+1),n∈N* . (Ⅰ)证明:数列{ ![]() }是等差数列;
}是等差数列;
(Ⅱ)设bn=3n ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则时速在[50,70)的汽车大约( ) 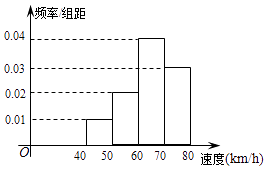
A.60辆
B.80辆
C.100辆
D.120辆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据). 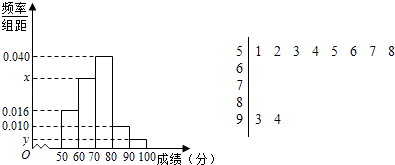
(1)求样本容量n和频率分布直方图中的x,y的值;
(2)估计本次竞赛学生成绩的中位数和平均分;
(3)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中至少有一人得分在[90,100]内的频率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]()
![]() 满足
满足![]() ,且
,且![]() ,正项数列
,正项数列![]() 满足
满足![]() ,其前7项和为42.
,其前7项和为42.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意正整数
,若对任意正整数![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)将数列![]() 的项按照“当
的项按照“当![]() 为奇数时,
为奇数时,![]() 放在前面;当
放在前面;当![]() 为偶数时,
为偶数时,![]() 放在前面”的要求进行排列,得到一个新的数列:
放在前面”的要求进行排列,得到一个新的数列:![]() ,求这个新数列的前
,求这个新数列的前![]() 项和
项和![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com