练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知正项等比数列{an}满足log2a1+log2a2+…+log2a2009=2009，则log2（a1+a2009）的最小值为 ．

    【答案】2
    【解析】解：∵log2a1+log2a2+…+log2a2009=2009由对数的运算性质可得，log2a1a2a2009=2009 ∴a1a2a2009=22009 ，
    由等比数列的性质可得，a1a2009=a2a2008=…=a10052 ，
    ∴a10052009=22009 ，
    ∵an＞0，
    ∴a1005=2，
    ∴a1a2009=a2a2008=…=a10052=4，
    由基本不等式可得，a1+a2009≥4，
    则log2（a1+a2019）≥2即最小值2，
    所以答案是：2．
    【考点精析】关于本题考查的等比数列的通项公式（及其变式），需要了解通项公式：才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】随着互联网的发展，移动支付（又称手机支付）越来越普通，某学校兴趣小组为了了解移动支付在大众中的熟知度，对15-65岁的人群随机抽样调查，调查的问题是“你会使用移动支付吗？”其中，回答“会”的共有个人.把这个人按照年龄分成5组：第1组，第2组，第3组，第4组，第5组，然后绘制成如图所示的频率分布直方图.其中，第一组的频数为20.

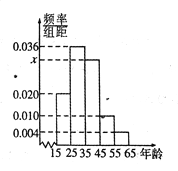
    （1）求 和的值，并根据频率分布直方图估计这组数据的众数；

    （2）从第1，3，4组中用分层抽样的方法抽取6人，求第1，3，4组抽取的人数；

    （3）在（2）抽取的6人中再随机抽取2人，求所抽取的2人来自同一个组的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知常数，解关于的不等式

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆：的左顶点为，右焦点为，上顶点为，下顶点为，若直线与直线的交点为．

    （1）求椭圆的标准方程；

    （2）点为椭圆的长轴上的一个动点，过点且斜率为的直线交椭圆于两点，证明：为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4－4：坐标系与参数方程

    在极坐标系中，曲线的极坐标方程是，以极点为原点，极轴为轴正半轴（两坐标系取相同的单位长度）的直角坐标系中，曲线的参数方程为：（为参数）．

    （1）求曲线的直角坐标方程与曲线的普通方程；

    （2）若用代换曲线的普通方程中的得到曲线的方程，若分别是曲线和曲线上的动点，求的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    某园艺公司种植了一批名贵树苗，为了解树苗的生长情况，从这批树苗中随机地测量了棵树苗的高度（单位：厘米），并把这些高度列成如下的频数分布表：

    组别

    频数

    2

    4

    11

    16

    13

    4

    （Ⅰ）在这批树苗中任取一棵，其高度在厘米以上的概率大约是多少？这批树苗的平均高度大约是多少？

    （Ⅱ）为了进一步获得研究资料，标记组中的树苗为，组中的树苗为，现从组中移出一棵树苗，从组中移出两棵树苗进行试验研究，则组的树苗和组的树苗同时被移出的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某食品厂定期购买面粉．已知该厂每天需用面粉6t，每吨面粉的价格为1800元，面粉的保管等其他费用为平均每吨每天3元，购面粉每次需支付运费900元．
    （1）求该厂多少天购买一次面粉，才能使平均每天所支付的总费用最少？
    （2）若提供面粉的公司规定：当一次购买面粉不少于210t时，其价格可享受9折优惠（即原价的90%），问该厂是否考虑利用此优惠条件？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在物理实验中，为了研究所挂物体的重量x对弹簧长度y的影响．某学生通过实验测量得到物体的重量与弹簧长度的对比表：

    物体重量（单位g）

    1

    2

    3

    4

    5

    弹簧长度（单位cm）

    1.5

    3

    4

    5

    6.5


    （1）画出散点图；
    （2）利用公式（公式见卷首）求y对x的回归直线方程；
    （3）预测所挂物体重量为8g时的弹簧长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4-4：坐标系与参数方程]

    以直角坐标系的原点为极点，轴的正半轴为极轴，且两个坐标系取相等的单位长度．已知直线的参数方程是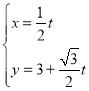（为参数），曲线的极坐标方程是．

    （1）写出直线的普通方程和曲线的直角坐标方程；

    （2）设直线与曲线相交于，两点，点为的中点，点的极坐标为，求的值．

    查看答案和解析>>

    同步练习册答案