
【题目】已知函数![]() ,直线
,直线![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)试确定曲线![]() 与直线
与直线![]() 的交点个数,并说明理由.
的交点个数,并说明理由.
【答案】(1)极小值![]() ,无极大值;(2)见解析.
,无极大值;(2)见解析.
【解析】
(1)求函数![]() 的导数,利用导数分析函数
的导数,利用导数分析函数![]() 的单调性,进而可得函数
的单调性,进而可得函数![]() 的极值;
的极值;
(2)令![]() ,利用参变量分离法得出
,利用参变量分离法得出![]() ,令
,令![]() ,设
,设![]() ,分析函数
,分析函数![]() 的单调性,从而确定
的单调性,从而确定![]() 在不同取值下两曲线交点的个数.
在不同取值下两曲线交点的个数.
(1)函数![]() 定义域为
定义域为![]() ,求导得
,求导得![]() ,令
,令![]() ,解得
,解得![]() .
.
列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
|
所以函数![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,单调减区间为
,单调减区间为![]() ,
,
所以函数![]() 有极小值
有极小值![]() ,无极大值;
,无极大值;
(2)“曲线![]() 与直线
与直线![]() 的交点个数”等价于“方程
的交点个数”等价于“方程![]() 的根的个数”,由方程
的根的个数”,由方程![]() ,得
,得![]() .
.
令![]() ,则
,则![]() ,其中
,其中![]() ,且
,且![]() ,
,
考查函数![]() ,其中
,其中![]() ,
,
因为![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,
,
而方程![]() 中,
中,![]() 且
且![]() ,
,
所以当![]() 时,方程
时,方程![]() 无根;
无根;
当![]() 时,方程
时,方程![]() 有且仅有一根,
有且仅有一根,
综上所述,当![]() 时,曲线
时,曲线![]() 与直线
与直线![]() 没有交点;
没有交点;
当![]() 时,曲线
时,曲线![]() 与直线
与直线![]() 有且仅有一个交点.
有且仅有一个交点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
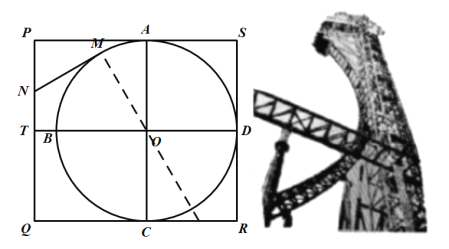
【题目】某游乐场过山车轨道在同一竖直钢架平面内,如图所示,矩形![]() 的长
的长![]() 为130米,宽
为130米,宽![]() 为120米,圆弧形轨道所在圆的圆心为0,圆O与
为120米,圆弧形轨道所在圆的圆心为0,圆O与![]() ,
,![]() ,
,![]() 分别相切于点A,D,CT为
分别相切于点A,D,CT为![]() 的中点.现欲设计过山车轨道,轨道由五段连接而成:出发点N在线段
的中点.现欲设计过山车轨道,轨道由五段连接而成:出发点N在线段![]() 上(不含端点,游客从点Q处乘升降电梯至点N),轨道第一段
上(不含端点,游客从点Q处乘升降电梯至点N),轨道第一段![]() 与圆O相切于点M,再沿着圆孤轨道
与圆O相切于点M,再沿着圆孤轨道![]() 到达最高点A,然后在点A处沿垂直轨道急速下降至点O处,接着沿直线轨道
到达最高点A,然后在点A处沿垂直轨道急速下降至点O处,接着沿直线轨道![]() 滑行至地面点G处(设计要求M,O,G三点共线),最后通过制动装置减速沿水平轨道
滑行至地面点G处(设计要求M,O,G三点共线),最后通过制动装置减速沿水平轨道![]() 滑行到达终点R记
滑行到达终点R记![]() 为
为![]() ,轨道总长度为l米.
,轨道总长度为l米.
(1)试将l表示为![]() 的函数
的函数![]() ,并写出
,并写出![]() 的取值范围;
的取值范围;
(2)求l最小时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】世界排球比赛一般实行“五局三胜制”,在2019年第13届世界女排俱乐部锦标赛(俗称世俱杯)中,中国女排和某国女排相遇,根据历年数据统计可知,在中国女排和该国女排的比赛中,每场比赛中国女排获胜的概率为![]() ,该国女排获胜的概率为
,该国女排获胜的概率为![]() ,现中国女排在先胜一局的情况下获胜的概率为( )
,现中国女排在先胜一局的情况下获胜的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中《方田》章有弧田面积计算问题,计算术曰:以弦乘矢,矢又自乘,并之,二而一.其大意是,弧田面积计算公式为:弧田面积![]() (弦乘矢+矢乘矢),弧田是由圆弧(简称为弧田的弧)和以圆弧的端点为端点的线段(简称 (弧田的弦)围成的平面图形,公式中“弦”指的是弧田的弦长,“矢”等于弧田的弧所在圆的半径与圆心到弧田的弦的距离之差.现有一弧田,其弦长
(弦乘矢+矢乘矢),弧田是由圆弧(简称为弧田的弧)和以圆弧的端点为端点的线段(简称 (弧田的弦)围成的平面图形,公式中“弦”指的是弧田的弦长,“矢”等于弧田的弧所在圆的半径与圆心到弧田的弦的距离之差.现有一弧田,其弦长![]() 等于
等于![]() ,其弧所在圆为圆
,其弧所在圆为圆![]() ,若用上述弧田面积计算公式计算得该弧田的面积为
,若用上述弧田面积计算公式计算得该弧田的面积为![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x﹣3|+|x+2|
(1)求不等式f(x)≤5的解集;
(2)若关于x的不等式f(x)≤a﹣|x|在区间[﹣1,2]上恒成立,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 交于点
交于点![]() ,曲线
,曲线![]() 与
与![]() 轴交于点
轴交于点![]() ,求线段
,求线段![]() 的中点到点
的中点到点![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com