
【题目】已知函数![]() .
.
(1)求![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)(i)若![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(i i)当![]() 时,证明
时,证明![]() .
.
【答案】(1)![]() ;(2)(i)
;(2)(i)![]() ;(i i)证明见解析.
;(i i)证明见解析.
【解析】
(1)对函数求导,求得![]() ,利用导数的几何意义,即可求得切线方程;
,利用导数的几何意义,即可求得切线方程;
(2)(i)将问题转化为![]() 恒成立,对参数
恒成立,对参数![]() 进行分类讨论,根据函数单调性,即可容易求参数的范围;
进行分类讨论,根据函数单调性,即可容易求参数的范围;
(i i)当![]() 时,
时,![]() ;结合(i)中所求,可得
;结合(i)中所求,可得![]() ,再利用不等式进行适度放缩,结合裂项求和,即可容易证明.
,再利用不等式进行适度放缩,结合裂项求和,即可容易证明.
(1)因为![]() ,
,
故可得![]() ,
,
![]() ,
,![]() ,
,
所以![]() 在点
在点![]() 处的切线方程为:
处的切线方程为:![]() ,
,
即![]() .
.
(2)(i)因为![]() 恒成立,
恒成立,
![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
令![]() ,则
,则![]() ,
,
①当![]() 时,
时,![]() ,所以
,所以![]() 满足;
满足;
②当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
因为![]() 时,
时,![]() ,所以
,所以![]() 不满足;
不满足;
③当![]() 时,
时,![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
![]() ,解得
,解得![]() .
.
所以![]() 的取值范围为
的取值范围为![]() .
.
(i i)![]() 时,
时,![]() ,所以
,所以![]() .
.
由(i)知:![]() ,即
,即![]() ,所以
,所以![]() .
.
令![]() ,得
,得![]() ,即
,即![]() ,所以
,所以![]() .
.
![]()
![]()
![]()
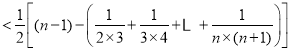
![]()
![]()
![]()
即证.


科目:高中数学 来源: 题型:
【题目】天津市某中学为全面贯彻“五育并举,立德树人”的教育方针,促进学生各科平衡发展,提升学生综合素养.该校教务处要求各班针对薄弱学科生成立特色学科“兴趣学习小组”(每位学生只能参加一个小组),以便课间学生进行相互帮扶.已知该校某班语文数学英语三个兴趣小组学生人数分别为10人10人15人.经过一段时间的学习,上学期期中考试中,他们的成绩有了明显进步.现采用分层抽样的方法从该班的语文,数学,英语三个兴趣小组中抽取7人,对期中考试这三科成绩及格情况进行调查.
(1)应从语文,数学,英语三个兴趣小组中分别抽取多少人?
(2)若抽取的7人中恰好有5人三科成绩全部及格,其余2人三科成绩不全及格.现从这7人中随机抽取4人做进一步的调查.
①记![]() 表示随机抽取4人中,语文,数学,英语三科成绩全及格的人数,求随机变量
表示随机抽取4人中,语文,数学,英语三科成绩全及格的人数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
②设![]() 为事件“抽取的4人中,有人成绩不全及格”,求事件
为事件“抽取的4人中,有人成绩不全及格”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px的焦点为F,过点F且斜率为1的直线l截得圆:x2+y2=p2的弦长为2![]() .
.
(1)求抛物线C的方程;
(2)若过点F作互相垂直的两条直线l1、l2,l1与抛物线C交于A、B两点,l2与抛物线C交于D、E两点,M、N分别为弦AB、DE的中点,求|MF||NF|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
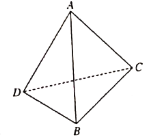
【题目】现有一副斜边长为10的直角三角板,将它们斜边![]() 重合,若将其中一个三角板沿斜边折起形成三棱锥
重合,若将其中一个三角板沿斜边折起形成三棱锥![]() ,如图所示,已知
,如图所示,已知![]() ,
,![]() ,则三棱锥
,则三棱锥![]() 的外接球的表面积为______;该三棱锥体积的最大值为_______.
的外接球的表面积为______;该三棱锥体积的最大值为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“柯西不等式”是由数学家柯西在研究数学分析中的“流数”问题时得到的,但从历史的角度讲,该不等式应当称为柯西﹣﹣布尼亚科夫斯基﹣﹣施瓦茨不等式,因为正是后两位数学家彼此独立地在积分学中推而广之,才将这一不等式推广到完善的地步,在高中数学选修教材4﹣5中给出了二维形式的柯西不等式:(a2+b2)(c2+d2)≥(ac+bd)2当且仅当ad=bc(即![]() )时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数
)时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数![]() 的最大值及取得最大值时x的值分别为( )
的最大值及取得最大值时x的值分别为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】干支历法是上古文明的产物,又称节气历或中国阳历,是一部深奥的历法.它是用60组各不相同的天干地支标记年月日时的历法.具体的算法如下:先用年份的尾数查出天干,如2013年3为癸;再用2013年除以12余数为9,9为巳.那么2013年就是癸巳年了,
天干 | 甲 | 乙 | 丙 | 丁 | 戊 | 己 | 庚 | 辛 | 壬 | 癸 | ||
4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | |||
地支 | 子 | 丑 | 寅 | 卯 | 辰 | 巳 | 午 | 未 | 申 | 酉 | 戌 | 亥 |
4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 1 | 2 | 3 |
2020年高三应届毕业生李东是壬午年出生,李东的父亲比他大25岁.问李东的父亲是哪一年出生( )
A.甲子B.乙丑C.丁巳D.丙卯
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com