
某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立.根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率依次为0.5, 0.6, 0.4.经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为0.6,0.5,0.75.
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为ξ,求随机变量ξ的期望.
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4 |
| 5 |
| 3 |
| 4 |
| 2 |
| 3 |
| 3 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立.根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率依次为![]() ,
,![]() ,
,![]() ,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为
,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为![]() ,
,![]() ,
,![]() .
.
(1)求第一次烧制后恰有一件产品合格的概率;(2)经过前后两次烧制后,合格工艺品的个数为![]() ,求随机变量
,求随机变量![]() 的期望.
的期望.
查看答案和解析>>
科目:高中数学 来源:2010年四川省成都石室中学高三第三次模拟考试(理) 题型:解答题
(12分)某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧作,两次烧制过程相互独立,根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率依次为0.5,0.6,0.4经 过第二
过第二 次烧制后,甲、乙、丙三件产品合格的概率依次为0.6,0.5,0.75。
次烧制后,甲、乙、丙三件产品合格的概率依次为0.6,0.5,0.75。
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为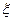 ,求随机变量
,求随机变量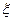 的期望。
的期望。
查看答案和解析>>
科目:高中数学 来源:2010-2011年广东省汕头市高二下学期期中考试理数 题型:解答题
(本小题满分12分)
某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立.根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率依次为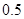 ,
,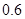 ,
,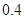 ,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为
,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为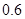 ,
,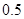 ,
,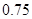 .
.
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为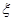 ,求随机变量
,求随机变量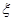 的期望.
的期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com