
【题目】已知函数![]() ,证明.
,证明.
(1)![]() 存在唯一的极小值点;
存在唯一的极小值点;
(2)![]() 的极小值点为
的极小值点为![]() 则
则![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)求出函数的导数并二次求导,即设![]() ,
,![]() ,结合余弦函数和指数函数的性质可求出当
,结合余弦函数和指数函数的性质可求出当![]() ,
,![]() 恒成立,即可判断出
恒成立,即可判断出![]() 在
在![]() 上的单调性,由零点存在定理可求出
上的单调性,由零点存在定理可求出![]() 在区间
在区间![]() 上存在唯一的零点
上存在唯一的零点![]() ,进而可证明结论.
,进而可证明结论.
(2)由![]() ,
,![]() ,由零点存在定理可得极小值点
,由零点存在定理可得极小值点![]() ,进而可得
,进而可得![]() ,结合三角恒等变换可得
,结合三角恒等变换可得![]()
![]() ,由正弦三角函数可求出
,由正弦三角函数可求出![]() .
.
解:(1)![]() ,设
,设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() ,
,
综上所述,当![]() ,
,![]() 恒成立,
恒成立,
故![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,由零点存在定理可知,
,由零点存在定理可知,
函数![]() 在区间
在区间![]() 上存在唯一的零点
上存在唯一的零点![]() ,
,![]() ,
,
结合单调性可得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以函数![]() 存在唯一极小值点
存在唯一极小值点![]() .
.
(2)由(1)知,![]() ,
,![]() ,
,
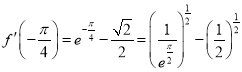 ,而
,而![]() ,所以
,所以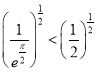 ,
,
即![]() ,
,![]() ,故极小值点
,故极小值点![]() ,
,
且![]() ,即
,即![]() ,由
,由![]() 式,得
式,得
![]()
![]() .由
.由![]() ,
,
得![]() ,所以
,所以![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】某校举办的体育节设有投篮项目.该项目规定:每位同学仅有三次投篮机会,其中前两次投篮每投中一次得1分,第三次投篮投中得2分,若不中不得分,投完三次后累计总分.
(1)若甲同学每次投篮命中的概率为![]() ,且相互不影响,记甲同学投完三次后的总分为X,求随机变量X的概率分布列;
,且相互不影响,记甲同学投完三次后的总分为X,求随机变量X的概率分布列;
(2)若(1)中的甲同学邀请乙同学一起参加投篮项目,已知乙同学每次投篮命中的概率为![]() ,且相互不影响,甲、乙两人之间互不干扰.求甲同学的总分低于乙同学的总分的概率.
,且相互不影响,甲、乙两人之间互不干扰.求甲同学的总分低于乙同学的总分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
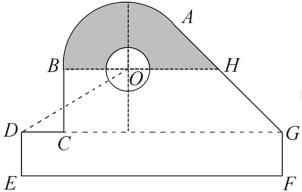
【题目】某中学开展劳动实习,学生加工制作零件,零件的截面如图所示.O为圆孔及轮廓圆弧AB所在圆的圆心,A是圆弧AB与直线AG的切点,B是圆弧AB与直线BC的切点,四边形DEFG为矩形,BC⊥DG,垂足为C,tan∠ODC=![]() ,
,![]() ,EF=12 cm,DE=2 cm,A到直线DE和EF的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为________cm2.
,EF=12 cm,DE=2 cm,A到直线DE和EF的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为________cm2.
查看答案和解析>>
科目:高中数学 来源: 题型:
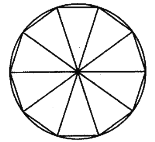
【题目】在3世纪中期,我国古代数学家刘徽在《九章算术注》中提出了割圆术:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这可视为中国古代极限观念的佳作.割圆术可以视为将一个圆内接正![]() 边形等分成
边形等分成![]() 个等腰三角形(如图所示),当
个等腰三角形(如图所示),当![]() 变得很大时,等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,可得到sin3°的近似值为( )(
变得很大时,等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,可得到sin3°的近似值为( )(![]() 取近似值3.14)
取近似值3.14)
A.0.012B.0.052
C.0.125D.0.235
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左焦点
的左焦点![]() ,点
,点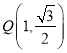 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)经过圆![]() :
:![]() 上一动点
上一动点![]() 作椭圆
作椭圆![]() 的两条切线,切点分别记为
的两条切线,切点分别记为![]() ,
,![]() ,直线
,直线![]() ,
,![]() 分别与圆
分别与圆![]() 相交于异于点
相交于异于点![]() 的
的![]() ,
,![]() 两点.
两点.
(i)当直线![]() ,
,![]() 的斜率都存在时,记直线
的斜率都存在时,记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .求证:
.求证:![]() ;
;
(ii)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为4的正三角形![]() 中,E为边
中,E为边![]() 的中点,过E作
的中点,过E作![]() 于D.把
于D.把![]() 沿
沿![]() 翻折至
翻折至![]() 的位置,连结
的位置,连结![]() .翻折过程中,其中正确的结论是( )
.翻折过程中,其中正确的结论是( )
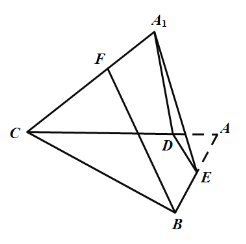
A.![]() ;
;
B.存在某个位置,使![]() ;
;
C.若![]() ,则
,则![]() 的长是定值;
的长是定值;
D.若![]() ,则四面体
,则四面体![]() 的体积最大值为
的体积最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系内,点A,B的坐标分别为![]() ,
,![]() ,P是坐标平面内的动点,且直线
,P是坐标平面内的动点,且直线![]() ,
,![]() 的斜率之积等于
的斜率之积等于![]() ,设点P的轨迹为C.
,设点P的轨迹为C.
(1)求轨迹C的方程;
(2)设过点![]() 且倾斜角不为0的直线
且倾斜角不为0的直线![]() 与轨迹C相交于M,N两点,求证:直线
与轨迹C相交于M,N两点,求证:直线![]() ,
,![]() 的交点在直线
的交点在直线![]() 上.
上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com