
【题目】在直角坐标系内,点A,B的坐标分别为![]() ,
,![]() ,P是坐标平面内的动点,且直线
,P是坐标平面内的动点,且直线![]() ,
,![]() 的斜率之积等于
的斜率之积等于![]() ,设点P的轨迹为C.
,设点P的轨迹为C.
(1)求轨迹C的方程;
(2)设过点![]() 且倾斜角不为0的直线
且倾斜角不为0的直线![]() 与轨迹C相交于M,N两点,求证:直线
与轨迹C相交于M,N两点,求证:直线![]() ,
,![]() 的交点在直线
的交点在直线![]() 上.
上.
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)过原点![]() 的直线
的直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与曲线
,与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() 为坐标原点,
为坐标原点, ![]() 是双曲线上在第一象限内的点,直线
是双曲线上在第一象限内的点,直线![]() 分别交双曲线
分别交双曲线![]() 左、右支于另一点
左、右支于另一点![]() ,
, ![]() ,且
,且![]() ,则双曲线
,则双曲线![]() 的离心率为( )
的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网络购物已经成为人们的一种生活方式.某购物平台为了给顾客提供更好的购物体验,为入驻商家设置了积分制度,每笔购物完成后,买家可以根据物流情况、商品质量等因素对商家做出评价,评价分为好评、中评和差评平台规定商家有50天的试营业时间,期间只评价不积分,正式营业后,每个好评给商家计1分,中评计0分,差评计![]() 分,某商家在试营业期间随机抽取100单交易调查了其商品的物流情况以及买家的评价情况,分别制成了图1和图2.
分,某商家在试营业期间随机抽取100单交易调查了其商品的物流情况以及买家的评价情况,分别制成了图1和图2.
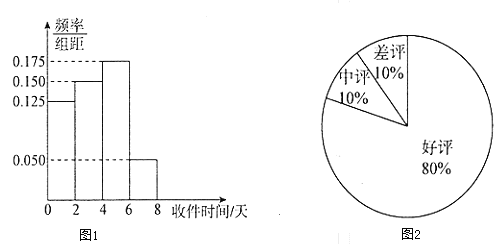
(1)通常收件时间不超过四天认为是物流迅速,否则认为是物流迟缓;
请根据题目所给信息完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“获得好评”与物流速度有关?
的把握认为“获得好评”与物流速度有关?
好评 | 中评或差评 | 合计 | |
物流迅速 | |||
物流迟缓 | 30 | ||
合计 |
(2)从正式营业开始,记商家在每笔交易中得到的评价得分为![]() .该商家将试营业50天期间的成交情况制成了频数分布表(表1),以试营业期间成交单数的频率代替正式营业时成交单数发生的概率.
.该商家将试营业50天期间的成交情况制成了频数分布表(表1),以试营业期间成交单数的频率代替正式营业时成交单数发生的概率.
表1
成交单数 | 36 | 30 | 27 |
天数 | 10 | 20 | 20 |
(Ⅰ)求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)平台规定,当积分超过10000分时,商家会获得“诚信商家”称号,请估计该商家从正式营业开始,1年内(365天)能否获得“诚信商家”称号
附: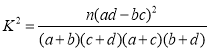
参考数据:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为梯形,
为梯形, ![]() ,且
,且![]() ,
, ![]() 是边长为2的正三角形,顶点
是边长为2的正三角形,顶点![]() 在
在![]() 上的射影为点
上的射影为点![]() ,且
,且![]() ,
, ![]() ,
, ![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是正三角形,CD平面PAD,E,F,G,O分别是PC,PD,BC,AD 的中点.
是正三角形,CD平面PAD,E,F,G,O分别是PC,PD,BC,AD 的中点.
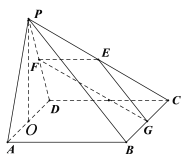
(Ⅰ)求证:PO平面![]() ;
;
(Ⅱ)求平面EFG与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,若存在,求线段
,若存在,求线段![]() 的长度;若不存在,说明理由.
的长度;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间用一台包装机包装葡萄糖,每袋葡萄糖的重量是一个随机变量,它服从正态分布.当机器工作正常时,每袋葡萄糖平均重量![]() 为0.5kg,标准差
为0.5kg,标准差![]() 为0.015kg.
为0.015kg.
(1)已知包装每袋葡萄糖的成本为1元,若发现包装好的葡萄糖重量异常,则需要将该袋葡萄糖进行重新包装,假设重新包装后的葡萄糖重量正常.若某袋葡萄糖的重量![]() 满足
满足![]() ,则认为该袋葡萄糖重量正常. 问:在机器工作正常的情况下,至少包装多少袋葡萄糖才能使“至少有一袋包装好的葡萄糖重量正常”的概率大于0.98?并求出相应成本的最小期望值.
,则认为该袋葡萄糖重量正常. 问:在机器工作正常的情况下,至少包装多少袋葡萄糖才能使“至少有一袋包装好的葡萄糖重量正常”的概率大于0.98?并求出相应成本的最小期望值.
(2)某日开工后, 为检査该包装机工作是否正常, 随机地抽取它所包装的葡萄糖9袋,若抽取的9袋葡萄糖称得净重(kg)为:0.496, 0.508, 0.524, 0.519, 0.495, 0.510, 0.522, 0.513, 0.512.用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,以
,以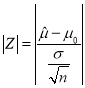 作为检验统计量,其中
作为检验统计量,其中![]() 为样本总数,
为样本总数,![]() 服从正态分布
服从正态分布![]() ,且
,且![]() .
.
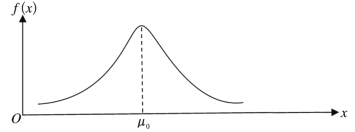
①若机器工作正常时, 每袋葡萄糖的重量服从的正态分布曲线如下图所示,且经计算得上述样本数据的标准差![]() 0.022.请在下图(机器正常工作时的正态分布曲线)中,绘制出以该样本作为估计得到的每袋葡萄糖所服从的正态分布曲线的草图.
0.022.请在下图(机器正常工作时的正态分布曲线)中,绘制出以该样本作为估计得到的每袋葡萄糖所服从的正态分布曲线的草图.
②若![]() ,就推断该包装机工作异常,这种推断犯错误的概率不超过
,就推断该包装机工作异常,这种推断犯错误的概率不超过![]() ,试以95%的可靠性估计该包装机工作是否正常.
,试以95%的可靠性估计该包装机工作是否正常.
附: 若随机变量![]() 服从正态分布:
服从正态分布:![]() ,
,![]()
![]()
参考数据:![]() ;
;![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列![]() 中,已知
中,已知![]() .在①
.在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个补充在第(2)问中,并对其求解.
这三个条件中任选一个补充在第(2)问中,并对其求解.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)若___________,求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com