
【题目】已知椭圆![]()
![]() 过点
过点![]() ,离心率为
,离心率为![]() ,
,![]() 分别为左右焦点.
分别为左右焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 上存在两个点
上存在两个点![]() ,椭圆上有两个点
,椭圆上有两个点![]() 满足
满足![]() 三点共线,
三点共线,![]() 三点共线,且
三点共线,且![]() ,求四边形
,求四边形![]() 面积的取值范围.
面积的取值范围.
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的方程:
的方程:![]()
(1)求m的取值范围;
(2)若圆C与直线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,求
,求![]() 的值
的值
(3)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂经过市场调查,甲产品的日销售量![]() (单位:吨)与销售价格
(单位:吨)与销售价格![]() (单位:万元/吨)满足关系式
(单位:万元/吨)满足关系式 (其中
(其中![]() 为常数),已知销售价格为
为常数),已知销售价格为![]() 万元/吨时,每天可售出该产品
万元/吨时,每天可售出该产品![]() 吨.
吨.
(1)求![]() 的值;
的值;
(2)若该产品的成本价格为![]() 万元/吨,当销售价格为多少时,该产品每天的利润最大?并求出最大值.
万元/吨,当销售价格为多少时,该产品每天的利润最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知平面![]() 平面
平面![]() ,四边形
,四边形![]() 是正方形,四边形
是正方形,四边形![]() 是菱形,且
是菱形,且![]() ,
,![]() ,点
,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的动点.
上的动点.
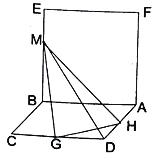
(1)求证:![]()
![]() ;
;
(2)求三棱锥![]() 的体积的最大值.
的体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次研究性学习有“整理数据”、“撰写报告”两项任务,两项任务无先后顺序,每项任务的完成相互独立,互不影响.某班研究性学习有甲、乙两个小组.根据以往资料统计,甲小组完成研究性学习两项任务的概率都为![]() ,乙小组完成研究性学习两项任务的概率都为
,乙小组完成研究性学习两项任务的概率都为![]() .若在一次研究性学习中,两个小组完成任务项数相等.而且两个小组完成任务数都不少于一项,则称该班为“和谐研究班”.
.若在一次研究性学习中,两个小组完成任务项数相等.而且两个小组完成任务数都不少于一项,则称该班为“和谐研究班”.
(1)若![]() ,求在一次研究性学习中,已知甲小组完成两项任务的条件下,该班荣获“和谐研究班”的概率;
,求在一次研究性学习中,已知甲小组完成两项任务的条件下,该班荣获“和谐研究班”的概率;
(2)设在完成4次研究性学习中该班获得“和谐研究班”的次数为![]() ,若
,若![]() 的数学期望
的数学期望![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
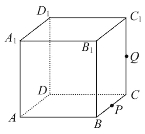
【题目】如图,正方体![]() 的棱长为1,P为BC的中点,Q为线段
的棱长为1,P为BC的中点,Q为线段![]() 上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是_________(写出所有正确命题的编号)。
上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是_________(写出所有正确命题的编号)。
①当![]() 时,S为四边形
时,S为四边形
②当![]() 时,S为等腰梯形
时,S为等腰梯形
③当![]() 时,S与
时,S与![]() 的交点R满足
的交点R满足![]()
④当![]() 时,S为六边形
时,S为六边形
⑤当![]() 时,S的面积为
时,S的面积为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若方程![]() 有两个小于2的不等实根,求实数a的取值范围;
有两个小于2的不等实根,求实数a的取值范围;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若函数![]() 在[0,2]上的最大值为4,求实数a的值.
在[0,2]上的最大值为4,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体![]() 的棱长为1,
的棱长为1,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,过直线
的中点,过直线![]() 的平面分别与棱
的平面分别与棱![]() 、
、![]() 交于
交于![]() ,设
,设![]() ,
,![]() ,给出以下四个命题:
,给出以下四个命题:
①四边形![]() 为平行四边形;
为平行四边形;
②若四边形![]() 面积
面积![]() ,
,![]() ,则
,则![]() 有最小值;
有最小值;
③若四棱锥![]() 的体积
的体积![]()
![]() ,
,![]() ,则
,则![]() 为常函数;
为常函数;
④若多面体![]() 的体积
的体积![]() ,
,![]() ,则
,则![]() 为单调函数.
为单调函数.
其中假命题为( )
A. ① ③ B. ② C. ③④ D. ④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com