
【题目】如图,四边形![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() ,
,![]() 都垂直于平面
都垂直于平面![]() ,且
,且![]() .
.
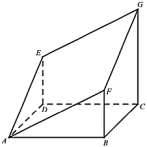
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)![]()
【解析】
(1)法一由![]() ,利用线面平行的判定定理,得到
,利用线面平行的判定定理,得到![]() 面
面![]() ,同理
,同理![]() 面
面![]() ,再由面面平行的判定定理得到面
,再由面面平行的判定定理得到面![]() 面
面![]() 即可.
即可.
(2)法一:连接![]() ,
,![]() 交于点
交于点![]() ,利用线面垂直的判定定理易得
,利用线面垂直的判定定理易得![]() 面
面![]() ,
,![]() 面
面![]() ,
,![]() 面
面![]() ,∴
,∴![]() ,又
,又![]() ,
,![]() ,四边形
,四边形![]() 为矩形,利用等体积法
为矩形,利用等体积法![]() 求解.
求解.
(1)法一∵![]() ,
,![]() 面
面![]() ,
,![]() 面
面![]() ,
,
∴![]() 面
面![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() 面
面![]() ,
,![]() 面
面![]() ,∴
,∴![]() 面
面![]() ,
,
∵![]() ,∴面
,∴面![]() 面
面![]() ,
,
又![]() 面
面![]() ,∴
,∴![]() 面
面![]() .
.
法二:取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,
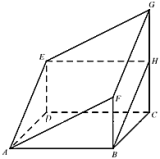
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,∴四边形
,∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,∴四边形
,∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,![]() 四点共面.
四点共面.
∴![]() 面
面![]() .
.
又![]() 面
面![]() ,∴
,∴![]() 面
面![]() .
.
(2)法一:连接![]() ,
,![]() 交于点
交于点![]() ,
,
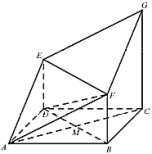
∵![]() 面
面![]() ,
,![]() 面
面![]() ,∴
,∴![]() .
.
又![]() ,
,![]() ,
,
∴![]() 面
面![]() .
.
在等边![]() 中,
中,![]() ,
,![]() ,
,
∵![]() 面
面![]() ,
,![]() 面
面![]() ,
,
∴![]() ,又
,又![]() ,
,![]() .
.
∴四边形![]() 为矩形,
为矩形,
∴![]() .
.
∴![]() .
.
法二:∵![]() 面
面![]() ,
,![]() 面
面![]() ,∴
,∴![]() ,
,
又![]() 面
面![]() ,
,![]() 面
面![]() ,
,
∴![]() 面
面![]() .
.
取![]() 中点
中点![]() ,连接
,连接![]() ,
,
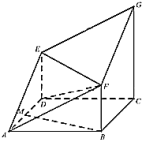
∵![]() 面
面![]() ,
,![]() 面
面![]() ,∴
,∴![]() ,
,
在等边![]() 中,
中,![]() ,
,
又![]() ,∴
,∴![]() 面
面![]() ,
,
∴![]() 到面
到面![]() 的距离即为
的距离即为![]() .
.
又![]() ,
,
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】自湖北武汉爆发新型冠状病毒肺炎疫情以来,各地医疗物资缺乏,各生产企业纷纷加班加点生产,某企业准备购买三台口罩生产设备,型号分别为A,B,C,已知这三台设备均使用同一种易耗品,提供设备的商家规定:可以在购买设备的同时购买该易耗品,每件易耗品的价格为100元;也可以在设备使用过程中,随时单独购买易耗品,每件易耗品的价格为200元.为了决策在购买设备时应同时购买的易耗品的件数,该单位调查了这三种型号的设备各60台,调查每台设备在一个月中使用的易耗品的件数,并得到统计表如下所示.
每台设备一个月中使用的易耗品的件数 | 6 | 7 | 8 | |
频数 | 型号A | 30 | 30 | 0 |
型号B | 20 | 30 | 10 | |
型号C | 0 | 45 | 15 | |
将调查的每种型号的设备的频率视为概率,各台设备在易耗品的使用上相互独立.
(1)求该单位一个月中A,B,C三台设备使用的易耗品总数超过21件(不包括21件)的概率;
(2)以该单位一个月购买易耗品所需总费用的期望值为决策依据,该单位在购买设备时应同时购买20件还是21件易耗品?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某动漫影视制作公司长期坚持文化自信,不断挖掘中华优秀传统文化中的动漫题材,创作出一批又一批的优秀动漫影视作品,获得市场和广大观众的一致好评,同时也为公司赢得丰厚的利润.该公司2013年至2019年的年利润![]() 关于年份代号
关于年份代号![]() 的统计数据如下表(已知该公司的年利润与年份代号线性相关):
的统计数据如下表(已知该公司的年利润与年份代号线性相关):
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
年利润 |
|
|
|
|
|
|
|
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程,并预测该公司2020年(年份代号记为
的线性回归方程,并预测该公司2020年(年份代号记为![]() )的年利润;
)的年利润;
(Ⅱ)当统计表中某年年利润的实际值大于由![]() 中线性回归方程计算出该年利润的估计值时,称该年为
中线性回归方程计算出该年利润的估计值时,称该年为![]() 级利润年,否则称为
级利润年,否则称为![]() 级利润年.将
级利润年.将![]() 中预测的该公司2020年的年利润视作该年利润的实际值,现从2015年至2020年这
中预测的该公司2020年的年利润视作该年利润的实际值,现从2015年至2020年这![]() 年中随机抽取
年中随机抽取![]() 年,求恰有
年,求恰有![]() 年为
年为![]() 级利润年的概率.
级利润年的概率.
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、点
、点![]() 及抛物线
及抛物线![]() .
.
(1)若直线![]() 过点
过点![]() 及抛物线
及抛物线![]() 上一点
上一点![]() ,当
,当![]() 最大时求直线
最大时求直线![]() 的方程;
的方程;
(2)![]() 轴上是否存在点
轴上是否存在点![]() ,使得过点
,使得过点![]() 的任一条直线与抛物线
的任一条直线与抛物线![]() 交于点
交于点![]() ,且点
,且点![]() 到直线
到直线![]() 的距离相等?若存在,求出点
的距离相等?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为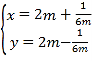 (m为参数),以坐标点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ+
(m为参数),以坐标点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ+![]() )=1.
)=1.
(1)求直线l的直角坐标方程和曲线C的普通方程;
(2)已知点M (2,0),若直线l与曲线C相交于P、Q两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是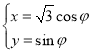 (
(![]() 为参数,
为参数,![]() ),在以坐标原点为极点,
),在以坐标原点为极点,![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,等边
,等边![]() 的顶点都在
的顶点都在![]() 上,且点
上,且点![]() ,
,![]() ,
,![]() 按照逆时针方向排列,点
按照逆时针方向排列,点![]() 的极坐标为
的极坐标为![]() .
.
(Ⅰ)求点![]() ,
,![]() ,
,![]() 的直角坐标;
的直角坐标;
(Ⅱ)设![]() 为
为![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为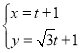 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知与直线![]() 平行的直线
平行的直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,试求
两点,试求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com