【题目】已知椭圆
，抛物线
的焦点均在
轴上， 
的中心和
的顶点均为原点
，从每条曲线上各取两个点，其坐标分别是
， 
， 
， 
．
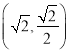（1）求
， 
的标准方程；
（2）是否存在直线
满足条件：①过
的焦点
；②与
交于不同的两点
且满足
？若存在，求出直线方程；若不存在，请说明理由．
【答案】（Ⅰ）
的标准方程为
； 
的标准方程为
；（Ⅱ）见解析.
【解析】试题分析：（1）设抛物线
，则有
，据此验证四个点即可求解（2）首先假设存在直线满足条件，利用向量垂直时
求出直线参数k即得结论
试题解析：
（Ⅰ）设抛物线
，则有
，
据此验证四个点知
， 
在抛物线上，
易得，抛物线
的标准方程为
设椭圆
，把点
， 
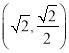代入可得
所以椭圆
的标准方程为
（Ⅱ）由椭圆的对称性可设
的焦点为F（1，0），
当直线l的斜率不存在时，直线l的方程为
直线l交椭圆
于点
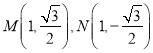
，不满足题意
当直线l的斜率存在时，设直线l的方程为
， 并设
由
，消去y得， 
，
于是
①，
由
得
②
将①代入②式，得
，解得
所以存在直线l满足条件，且l的方程为
或
科目：高中数学 来源： 题型：
【题目】已知函数 
，其中a∈R，若对任意的非零的实数x1 ， 存在唯一的非零的实数x2（x2≠x1），使得f（x2）=f（x1）成立，则k的最小值为（ ）
A.
B.5
C.6
D.8
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】中秋节即将到来，为了做好中秋节商场促销活动，某商场打算将进行促销活动的礼品盒重新设计．方案如下：将一块边长为10的正方形纸片
剪去四个全等的等腰三角形
， 
， 
， 
再将剩下的阴影部分折成一个四棱锥形状的包装盒
，其中
重合于点
， 
与
重合， 
与
重合， 
与
重合， 
与
重合（如图所示）．
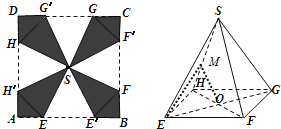
（1）求证：平面
平面
；
（2）已知
，过
作
交
于点
，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知集合A={x|2a≤x＜a+3}，B={x|x＜﹣1或x＞5}．
（1）若a=﹣1，求A∪B，（RA）∩B．
（2）若A∩B=，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数 
．
（1）判断并证明函数f（x）的奇偶性
（2）判断并证明当x∈（﹣1，1）时函数f（x）的单调性；
（3）在（2）成立的条件下，解不等式f（2x﹣1）+f（x）＜0．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
