
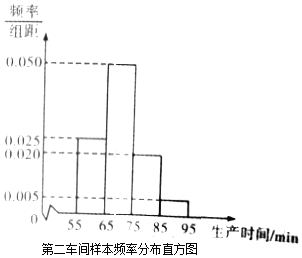
【题目】某工厂有两个车间生产同一种产品,第一车间有工人200人,第二车间有工人400人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,并对他们中每位工人生产完成一件产品的时间(单位:min)分别进行统计,得到下列统计图表(按照[55,65),[65,75),[75,85),[85,95]分组).
分组 | 频数 |
[55,65) | 2 |
[65,75) | 4 |
[75,85) | 10 |
[85,95] | 4 |
合计 | 20 |
第一车间样本频数分布表
(Ⅰ)分别估计两个车间工人中,生产一件产品时间小于75min的人数;
(Ⅱ)分别估计两车间工人生产时间的平均值,并推测哪个车间工人的生产效率更高?(同一组中的数据以这组数据所在区间中点的值作代表)
(Ⅲ)从第一车间被统计的生产时间小于75min的工人中,随机抽取3人,记抽取的生产时间小于65min的工人人数为随机变量X,求X的分布列及数学期望.
【答案】(I)60,300;(II)第二车间工人生产效率更高.(III)见解析.
【解析】
(I)估计第一车间生产时间小于75min的工人人数为![]() (人).估计第二车间生产时间小于75min的工人人数为
(人).估计第二车间生产时间小于75min的工人人数为![]() (人);(II)分别计算两车间工人生产时间的平均值,再推测哪个车间工人的生产效率更高;(III)由题得X可取值为0,1,2,再分别求出概率,列出分布列,求出数学期望.
(人);(II)分别计算两车间工人生产时间的平均值,再推测哪个车间工人的生产效率更高;(III)由题得X可取值为0,1,2,再分别求出概率,列出分布列,求出数学期望.
(I)估计第一车间生产时间小于75min的工人人数为![]() (人).
(人).
估计第二车间生产时间小于75min的工人人数为![]() (人).
(人).
(II)第一车间生产时间平均值约为![]() (min).
(min).
第二车间生产时间平均值约为![]()
(min).
∴第二车间工人生产效率更高.
(III)由题意得,第一车间被统计的生产时间小于75min的工人有6人,其中生产时间小于65min的有2人,从中抽取3人,随机变量X服从超几何分布,
X可取值为0,1,2,
![]() ,
,
![]() ,
,
![]() .
.
X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
所以数学期望![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
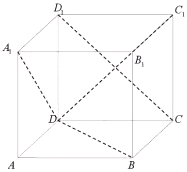
【题目】如图,![]() 的棱长为1的正方体,任作平面
的棱长为1的正方体,任作平面![]() 与对角线
与对角线![]() 垂直,使得
垂直,使得![]() 与正方体的每个面都有公共点,这样得到的截面多边形的面积为
与正方体的每个面都有公共点,这样得到的截面多边形的面积为![]() ,周长为
,周长为![]() 的范围分别是_____________(用集合表示)
的范围分别是_____________(用集合表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位全体员工年龄频率分布表,经统计,该单位35岁以下的青年职工中,男职工和女职工人数相等,且男职工的年龄频率分布直方图和如下:
年龄(岁) | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) | [50,55) | 合计 |
人数(人) | 6 | 18 | 50 | 31 | 19 | 16 | 140 |
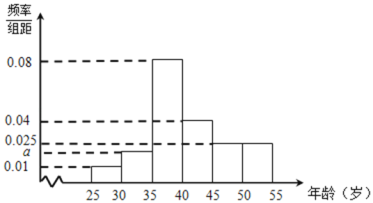
(Ⅰ)求![]() ;
;
(Ⅱ)求该单位男女职工的比例;
(Ⅲ)若从年龄在[25,30)岁的职工中随机抽取两人参加某项活动,求恰好抽取一名男职工和一名女职工的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有标号为![]() 的
的![]() 张标签,随机的选取两张标签.
张标签,随机的选取两张标签.
(1)若标签的选取是无放回的,求两张标签上的数字为相邻整数的概率;
(2)若标签的选取是有放回的,求两张标签上的数字至少有一个为5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中
①.对于命题![]() :存在
:存在![]() ,则
,则![]() :
:![]() ;
;
②.命题“若![]() ,则函数
,则函数![]() 在
在![]() 上是增函数”的逆命题为假命题;
上是增函数”的逆命题为假命题;
③.若![]() 为真命题,则
为真命题,则![]() 均为真命题;
均为真命题;
④.命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”.
”.
错误的是________
查看答案和解析>>
科目:高中数学 来源: 题型:
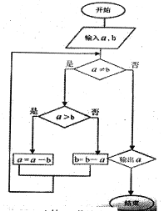
【题目】《九章算术》是中国古代第一部数学专著,全书总结了战国、秦、汉时期的数学成就。“更相减损术”便出自其中,原文记载如下:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也。”其核心思想编译成如示框图,若输入的![]() ,
,![]() 分别为45,63,则输出的
分别为45,63,则输出的![]() 为( )
为( )
A. 2B. 3C. 5D. 9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是圆锥的高,
是圆锥的高,![]() 是圆锥底面的直径,
是圆锥底面的直径,![]() 是底面圆周上一点,
是底面圆周上一点,![]() 是
是![]() 的中点,平面
的中点,平面![]() 和平面
和平面![]() 将圆锥截去部分后的几何体如图所示.
将圆锥截去部分后的几何体如图所示.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以平面直角坐标系的原点为极点,
),以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 被圆截得的弦长为
被圆截得的弦长为![]() 时,求
时,求![]() 的值.
的值.
(2)直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),若
为参数),若![]() ,垂足为
,垂足为![]() ,求
,求![]() 点的极坐标.
点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.回归直线过样本点的中心![]() .
.
B.对分类变量X与Y,随机变量K2的观测值k越大,则判断“X与Y有关系”的把握程度越小
C.两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1
D.在回归直线方程![]() =0.2x+0.8中,当解释变量x每增加1个单位时,预报变量
=0.2x+0.8中,当解释变量x每增加1个单位时,预报变量![]() 平均增加0.2个单位
平均增加0.2个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com