
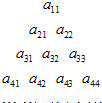
 个,由此可得 aii 的值.
个,由此可得 aii 的值. 个,∴aii =2×
个,∴aii =2× =i(i+1)=i2+i,
=i(i+1)=i2+i, ,∴m+n=5,
,∴m+n=5,

科目:高中数学 来源: 题型:
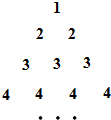 将如图所示的三角形数阵中的数按从小到大的顺序排列:1,2,2,3,3,3,4,4,4,4,…,记为数列{an},记数列{an}前2k2(k∈N+)项的和为bk,可以推测:
将如图所示的三角形数阵中的数按从小到大的顺序排列:1,2,2,3,3,3,4,4,4,4,…,记为数列{an},记数列{an}前2k2(k∈N+)项的和为bk,可以推测:| 1 |
| 6 |
| 1 |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
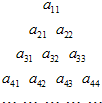 将如图所示的三角形数阵中所有的数按从上至下、从左至右的顺序排列成数列a11,a21,a22,a31,a32,….若所得数列构成一个等差数列,且a11=2,a33=12,则
将如图所示的三角形数阵中所有的数按从上至下、从左至右的顺序排列成数列a11,a21,a22,a31,a32,….若所得数列构成一个等差数列,且a11=2,a33=12,则查看答案和解析>>
科目:高中数学 来源: 题型:
将如图所示的三角形数阵中所有的数按从上至下、从左至右的顺序排列成数列a11,a21,a22,a31,a32,….若所得数列构成一个等差数列,且a11=2,a33=12,则
①数阵中的数aii可用i表示为 ;
②若amn+a(m+1)(n+1)=a(m+2)(n+2),则m+n的值为 .
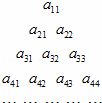
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com