
【题目】己知数列{an}的前n项和Sn= ![]() ,n∈N* .
,n∈N* .
(1)求数列{an}的通项公式;
(2)设bn=2an+(﹣1)nan , 求数列{bn}的前2n项和.
【答案】
(1)解:Sn= ![]() ,n∈N*,
,n∈N*,
可得a1=S1=1,
当n>1时,an=Sn﹣Sn﹣1= ![]() ﹣
﹣ ![]() =n,
=n,
综上可得,an=n,n∈N*
(2)解:bn=2n+(﹣1)nn,
n为奇数时,bn=n;n为偶数时,bn=3n.
即有数列{bn}的前2n项和为(1+3+5+…+2n﹣1)+(6+12+…+6n)
= ![]() n(1+2n﹣1)+
n(1+2n﹣1)+ ![]() n(6+6n)=3n2+4n
n(6+6n)=3n2+4n
【解析】(1)求得首项,再由n换为n﹣1,相减可得数列的通项公式;(2)求得bn=2n+(﹣1)nn,n为奇数时,bn=n;n为偶数时,bn=3n.运用等差数列的求和公式计算即可得到所求.
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系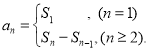 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
【题目】“城市呼唤绿化”,发展园林绿化事业是促进国家经济法阵和城市建设事业的重要组成部分,某城市响应城市绿化的号召,计划建一如图所示的三角形ABC形状的主题公园,其中一边利用现成的围墙BC,长度为100 ![]() 米,另外两边AB,AC使用某种新型材料围成,已知∠BAC=120°,AB=x,AC=y(x,y单位均为米).
米,另外两边AB,AC使用某种新型材料围成,已知∠BAC=120°,AB=x,AC=y(x,y单位均为米). 
(1)求x,y满足的关系式(指出x,y的取值范围);
(2)在保证围成的是三角形公园的情况下,如何设计能使所用的新型材料总长度最短?最短长度是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,若A,B,C成等差数列,2a,2b,2c成等比数列,则cosAcosB=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式kx2﹣2x+3k<0.
(1)若不等式的解集为{x|x<﹣3或x>﹣1},求k的值;
(2)若不等式的解集为,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015男篮亚锦赛决赛阶段,中国男篮以![]() 连胜的不败成绩赢得第
连胜的不败成绩赢得第![]() 届亚锦赛冠军,同时拿到亚洲唯一
届亚锦赛冠军,同时拿到亚洲唯一![]() 张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛
张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛![]() (最有价值球员),下表是易建联在这
(最有价值球员),下表是易建联在这![]() 场比赛中投篮的统计数据.
场比赛中投篮的统计数据.
比分 | 易建联技术统计 | |||
投篮命中 | 罚球命中 | 全场得分 | 真实得分率 | |
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
注:(1)表中![]() 表示出手
表示出手![]() 次命中
次命中![]() 次;
次;
(2)![]() (真实得分率)是衡量球员进攻的效率,其计算公式为:
(真实得分率)是衡量球员进攻的效率,其计算公式为:
![]()
(1)从上述![]() 场比赛中随机选择一场,求易建联在该场比赛中
场比赛中随机选择一场,求易建联在该场比赛中![]() 超过
超过![]() 的概率;
的概率;
(2)我们把比分分差不超过![]() 分的比赛称为“胶着比赛”.为了考验求易建联在“胶着比赛”中的发挥情况,从“胶着比赛”中随机选择两场,求易建联在这两场比赛中
分的比赛称为“胶着比赛”.为了考验求易建联在“胶着比赛”中的发挥情况,从“胶着比赛”中随机选择两场,求易建联在这两场比赛中![]() 至少有一场超过
至少有一场超过![]() 的概率;
的概率;
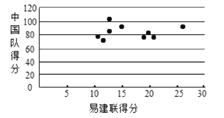
(3)用![]() 来表示易建联某场的得分,用
来表示易建联某场的得分,用![]() 来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断
来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断![]() 与
与![]() 之间是否具有线性相关关系?结合实际简单说明理由.
之间是否具有线性相关关系?结合实际简单说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 的坐标分别为
的坐标分别为![]() ,直线
,直线![]() 相交于点
相交于点![]() ,且它们的斜率之积是
,且它们的斜率之积是![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() 是否存在实数
是否存在实数![]() ,使得
,使得![]() 的面积为
的面积为![]() ?若存在,请求出
?若存在,请求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2,﹣3),
=(2,﹣3), ![]() =(﹣5,4),
=(﹣5,4), ![]() =(1﹣λ,3λ+2).
=(1﹣λ,3λ+2).
(1)若△ABC为直角三角形,且∠B为直角,求实数λ的值;
(2)若点A、B、C能构成三角形,求实数λ应满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,网格纸上小正方形的边长为1,粗线画出的是某个四面体的三视图,则该四面体的表面积为( ) 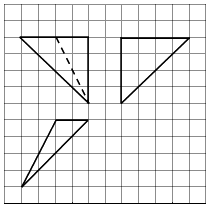
A.8+8 ![]() +4
+4 ![]()
B.8+8 ![]() +2
+2 ![]()
C.2+2 ![]() +
+ ![]()
D.![]() +
+ ![]() +
+ ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com