
【题目】已知函数![]()
(Ⅰ)求函数![]() 的图像在点
的图像在点![]() 处的切线方程.
处的切线方程.
(Ⅱ)若![]() 且
且![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的最大值;
的最大值;
(Ⅲ)当![]() 时,证明:
时,证明:![]()
【答案】(Ⅰ)![]() ;(Ⅱ)3;(Ⅲ)证明见解析.
;(Ⅱ)3;(Ⅲ)证明见解析.
【解析】
(Ⅰ)首先求得导函数的解析式,据此可得切线的斜率,然后求解切线方程即可;
(Ⅱ)将原问题转化为函数在给定区间上恒成立的问题,构造新函数,结合函数的单调性和零点存在定理即可确定![]() 的最大值;
的最大值;
(Ⅲ)结合(Ⅱ)中证得的函数单调性和不等式的性质得到关于m,n的不等式,对不等式进行整理变形即可证得题中的结论.
(Ⅰ)因为![]() ,所以
,所以![]() ,
,
函数![]() 的图像在点
的图像在点![]() 处的切线方程
处的切线方程![]() ;
;
(Ⅱ)由题意可知![]() 对任意
对任意![]() 恒成立即
恒成立即![]() 对任意
对任意![]() 恒成立.
恒成立.
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,
因为![]() ,
,![]() ,
,
所以方程![]() 在
在![]() 上存在唯一实根
上存在唯一实根![]() ,
,
且满足![]() .
.
当![]() 时,
时,![]() 即
即![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以:
上单调递增,所以:
![]() ,
,
所以![]() ,故整数
,故整数![]() 的最大值是3.
的最大值是3.
(Ⅲ)由(Ⅱ)知,![]() 是
是![]() 上的增函数,
上的增函数,
所以当![]() 时,
时,![]() 即
即![]() ,
,
整理得![]() ,
,
因为![]() ,故
,故![]() ,
,
所以![]() ,
,
即![]() ,
,
即![]() ,
,
所以![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】“五一”期间,甲乙两个商场分别开展促销活动.
(Ⅰ)甲商场的规则是:凡购物满100元,可抽奖一次,从装有大小、形状相同的4个白球、4个黑球的袋中摸出4个球,中奖情况如下表:
摸出的结果 | 获得奖金(单位:元) |
4个白球或4个黑球 | 200 |
3个白球1个黑球或3个黑球1个白球 | 20 |
2个黑球2个白球 | 10 |
记![]() 为抽奖一次获得的奖金,求
为抽奖一次获得的奖金,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)乙商场的规则是:凡购物满100元,可抽奖10次.其中,第![]() 次抽奖方法是:从编号为
次抽奖方法是:从编号为![]() 的袋中(装有大小、形状相同的
的袋中(装有大小、形状相同的![]() 个白球和
个白球和![]() 个黑球)摸出
个黑球)摸出![]() 个球,若该次摸出的
个球,若该次摸出的![]() 个球颜色都相同,则可获得奖金
个球颜色都相同,则可获得奖金![]() 元;记第
元;记第![]() 次获奖概率
次获奖概率![]() .设各次摸奖的结果互不影响,最终所获得的总奖金为10次奖金之和.
.设各次摸奖的结果互不影响,最终所获得的总奖金为10次奖金之和.
①求证:![]() ;
;
②若某顾客购买120元的商品,不考虑其它因素,从获得奖金的期望分析,他应该选择哪一家商场?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(I)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.
(i)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;
(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题:
①“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
②“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
③若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题
均为假命题
④对于命题![]() :
:![]() ,
,![]() ,则
,则![]() 为:
为:![]() ,
,![]()
其中真命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
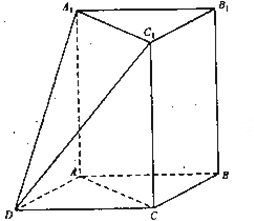
【题目】如图,三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,以
,以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,连接
,连接![]() 和
和![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 与平面
与平面![]() 垂直?若存在,求出
垂直?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通指数是指交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念性指数值,记交通指数为![]() ,其范围为
,其范围为![]() ,分别有五个级别:
,分别有五个级别:![]() ,畅通;
,畅通;![]() ,基本畅通;
,基本畅通;![]() ,轻度拥堵;
,轻度拥堵;![]() ,中度拥堵;
,中度拥堵;![]() ,严重拥堵.在晚高峰时段(
,严重拥堵.在晚高峰时段(![]() ),从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制的频率分布直方图如图所示.
),从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制的频率分布直方图如图所示.

(1)求出轻度拥堵、中度拥堵、严重拥堵的路段的个数;
(2)用分层抽样的方法从轻度拥堵、中度拥堵、严重拥堵的路段中共抽取6个路段,求依次抽取的三个级别路段的个数;
(3)从(2)中抽取的6个路段中任取2个,求至少有1个路段为轻度拥堵的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研小组研究发现:一棵水蜜桃树的产量![]() (单位:百千克)与肥料费用
(单位:百千克)与肥料费用![]() (单位:百元)满足如下关系:
(单位:百元)满足如下关系:![]() ,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)
,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)![]() 百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为
百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求利润函数![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(2)当投入的肥料费用为多少时,该水蜜桃树获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的各项排成如图所示的三角形数阵,数阵中每一行的第一个数
的各项排成如图所示的三角形数阵,数阵中每一行的第一个数![]() 构成等差数列
构成等差数列![]() ,
,![]() 是
是![]() 的前
的前![]() 项和,且
项和,且![]() ,
,![]() .
.
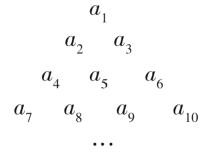
(1)若数阵中从第3行开始每行中的数按从左到右的顺序均构成公比为正数的等比数列,且公比相等,已知![]() ,求
,求![]() 的值;
的值;
(2)设![]() ,当
,当![]() 时,对任意
时,对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com