
【题目】某超市从2014年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,整理得到数据分组及频率分布表和频率分布直方图:
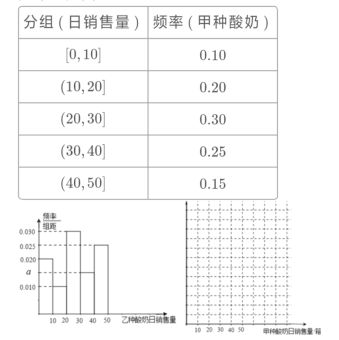
(1)写出频率分布直方图中![]() 的值,并做出甲种酸奶日销售量的频率分布直方图;
的值,并做出甲种酸奶日销售量的频率分布直方图;
(2)记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为![]() 。试比较
。试比较![]() 和
和![]() 的大小
的大小
(3)假设同一组中的每个数据可用该组区间的中间值代替,试估计乙种酸奶在未来一个月(按30天计算)的销售总量
【答案】(1) ![]() ,频率分布直方图见解析;(2)
,频率分布直方图见解析;(2) ![]() (3)795箱
(3)795箱
【解析】
(1)根据频率之和为1,结合乙的频率分布直方图即可求出![]() ;根据题中数据可直接完善甲的频率分布直方图;
;根据题中数据可直接完善甲的频率分布直方图;
(2)解法一:由方差的计算公式,分别求出两种酸奶的方差,比较大小,即可得出结果;
解法二:根据频率分布的特征,数据越集中,方差越小,即可得出结果;
(3)根据乙的频率分布直方图,每组中间值乘以该组的频率、再求和,进而可得出平均数,预测出总销量.
(1)由乙种酸奶日销量的频率分布直方图可得:
![]()
根据题中数据可得,甲种酸奶日销售量的频率分布直方图如下:

(2)解法一:
记甲乙两种酸奶日销售量的平均数分别为![]() ,
,![]() ,
,
由频率分布直方图可得:
![]() ,
,
![]() ,
,
所以![]()
![]() ;
;
![]()
![]() ;
;
所以![]() ;
;
解法二:
比较两种酸奶的频率分布直方图,数据越集中,则方差越小,由频率分布直方图可得,
甲酸奶对应的数据更集中,故甲的方差小于乙的方差;
即![]() ;
;
(3)乙种酸奶的平均日销售量为:
![]() (箱)
(箱)
乙种酸奶未来一个月的销售量为![]() (箱)
(箱)


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
【题目】从高三学生中抽取![]() 名学生参加数学竞赛,成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间
名学生参加数学竞赛,成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间![]() ,且成绩在区间
,且成绩在区间![]() 的学生人数是
的学生人数是![]() 人.
人.

(1)求![]() ,
,![]() 的值;
的值;
(2)若从数学成绩(单位:分)在![]() 的学生中随机选取
的学生中随机选取![]() 人进行成绩分析.
人进行成绩分析.
①列出所有可能的抽取结果;
②设选取的![]() 人中,成绩都在
人中,成绩都在![]() 内为事件
内为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义在[0,2]上的增函数,且图像是连续不断的曲线,若f(0)=M,f(2)=N(M>0,N>0),那么下列四个命题中是真命题的有( )
A.必存在x∈[0,2],使得f(x)![]() B.必存在x∈[0,2],使得f(x)
B.必存在x∈[0,2],使得f(x)![]()
C.必存在x∈[0,2],使得f(x)![]() D.必存在x∈[0,2],使得f(x)
D.必存在x∈[0,2],使得f(x)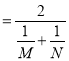
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2-5ax+4a2<0(其中a>0),q:实数x满足2<x≤5.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若![]() q是
q是![]() p的必要不充分条件,求实数a的取值范围.
p的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的方程为
的方程为![]() ,其焦点为
,其焦点为![]() ,
,![]() 为过焦点
为过焦点![]() 的抛物线
的抛物线![]() 的弦,过
的弦,过![]() 分别作抛物线的切线
分别作抛物线的切线![]() ,设
,设![]() 相交于点
相交于点![]() .
.
(1)求![]() 的值;
的值;
(2)如果圆![]() 的方程为
的方程为![]() ,且点
,且点![]() 在圆
在圆![]() 内部,设直线
内部,设直线![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() 上两点,且
上两点,且![]() ,给出下列四个命题:①三棱锥
,给出下列四个命题:①三棱锥![]() 的体积为定值;②异面直线
的体积为定值;②异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ;③
;③![]() 平面
平面![]() ;④直线
;④直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .其中正确的命题为( )
.其中正确的命题为( )
A. ①② B. ②③ C. ①②④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 经过点
经过点![]() ,离心率为
,离心率为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过![]() 的左焦点
的左焦点![]() 且斜率不为
且斜率不为![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,若
,若![]() 为等腰直角三角形,求
为等腰直角三角形,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴的极坐标中,圆
轴正半轴为极轴的极坐标中,圆![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的坐标为
的坐标为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com