
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴的极坐标中,圆
轴正半轴为极轴的极坐标中,圆![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的坐标为
的坐标为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题(1)由加减消元得直线![]() 的普通方程,由
的普通方程,由![]() 得圆
得圆![]() 的直角坐标方程;(2)把直线l的参数方程代入圆C的直角坐标方程,由直线参数方程几何意义得|PA|+|PB|=|t1|+|t2|=t1+t2,再根据韦达定理可得结果
的直角坐标方程;(2)把直线l的参数方程代入圆C的直角坐标方程,由直线参数方程几何意义得|PA|+|PB|=|t1|+|t2|=t1+t2,再根据韦达定理可得结果
试题解析:解:(Ⅰ)由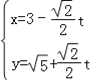 得直线l的普通方程为x+y﹣3﹣
得直线l的普通方程为x+y﹣3﹣![]() =0
=0
又由![]() 得 ρ2=2
得 ρ2=2![]() ρsinθ,化为直角坐标方程为x2+(y﹣
ρsinθ,化为直角坐标方程为x2+(y﹣![]() )2=5;
)2=5;
(Ⅱ)把直线l的参数方程代入圆C的直角坐标方程,
得(3﹣![]() t)2+(
t)2+(![]() t)2=5,即t2﹣3
t)2=5,即t2﹣3![]() t+4=0
t+4=0
设t1,t2是上述方程的两实数根,
所以t1+t2=3![]()
又直线l过点P![]() ,A、B两点对应的参数分别为t1,t2,
,A、B两点对应的参数分别为t1,t2,
所以|PA|+|PB|=|t1|+|t2|=t1+t2=3![]() .
.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】某超市从2014年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,整理得到数据分组及频率分布表和频率分布直方图:
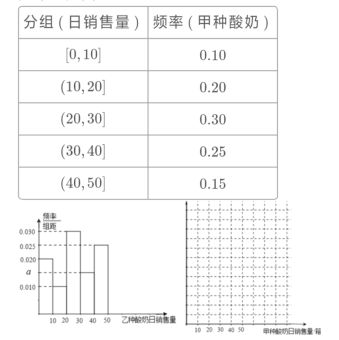
(1)写出频率分布直方图中![]() 的值,并做出甲种酸奶日销售量的频率分布直方图;
的值,并做出甲种酸奶日销售量的频率分布直方图;
(2)记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为![]() 。试比较
。试比较![]() 和
和![]() 的大小
的大小
(3)假设同一组中的每个数据可用该组区间的中间值代替,试估计乙种酸奶在未来一个月(按30天计算)的销售总量
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱台![]() 中,上底面边长为4,下底面边长为8,高为5,点
中,上底面边长为4,下底面边长为8,高为5,点![]() 分别在
分别在![]() 上,且
上,且![]() .过点
.过点![]() 的平面
的平面![]() 与此四棱台的下底面会相交,则平面
与此四棱台的下底面会相交,则平面![]() 与四棱台的面的交线所围成图形的面积的最大值为
与四棱台的面的交线所围成图形的面积的最大值为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 且垂直于
且垂直于![]() 轴的直线交椭圆
轴的直线交椭圆![]() 于
于![]() 两点,且
两点,且![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)若直线![]() 是圆
是圆![]() 上的点
上的点![]() 处的切线,点
处的切线,点![]() 是直线
是直线![]() 上任一点,过点
上任一点,过点![]() 作椭圆
作椭圆![]() 的切线
的切线![]() ,切点分别为
,切点分别为![]() ,设切线的斜率都存在.求证:直线
,设切线的斜率都存在.求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 的各条棱长均相等,
的各条棱长均相等, ![]() 为
为![]() 的中点,
的中点, ![]() 分别是线段
分别是线段![]() 和线段
和线段![]() 上的动点(含端点),且满足
上的动点(含端点),且满足![]() .当
.当![]() 运动时,下列结论中不正确的是( )
运动时,下列结论中不正确的是( )

A. 平面![]() 平面
平面![]() B. 三棱锥
B. 三棱锥![]() 的体积为定值
的体积为定值
C. ![]() 可能为直角三角形 D. 平面
可能为直角三角形 D. 平面![]() 与平面
与平面![]() 所成的锐二面角范围为
所成的锐二面角范围为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高二年级有男生490人,女生510人,张华按男生、女生进行分层,通过分层随机抽样的方法,得到男生、女生的平均身高分别为170.2cm和160.8cm.
(1)如果张华在各层中按比例分配样本,总样本量为100,那么在男生、女生中分别抽取了多少名?在这种情况下,请估计高二年级全体学生的平均身高.
(2)如果张华从男生、女生中抽取的样本量分别为30和70,那么在这种情况下,如何估计高二年级全体学生的平均身高更合理?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲一中某研究性学习小组对学习数学的练习时间与进步率的关系进行研究,他们分别记录了同班5个同学一周内的学习时间与周测成绩进步率,得到如下资料.

(1)从5个同学中任选2个,记其进步率分别为![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2)若进步率![]() 与学习时间
与学习时间![]() 服从线性关系,求出
服从线性关系,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)在这5个同学中任取3个,其中进步率超过25的有![]() 个同学,求
个同学,求![]() 的数学期望.
的数学期望.
参考公式:回归直线方程是![]() ,其中
,其中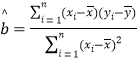
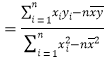
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数(简称:![]() )是定量描述空气质量状况的无量纲指数,空气质量按照
)是定量描述空气质量状况的无量纲指数,空气质量按照![]() 大小分为六级:
大小分为六级:![]() 为优,
为优,![]() 为良,
为良,![]() 为轻度污染,
为轻度污染,![]() 为中度污染,
为中度污染,![]() 为重度污染,
为重度污染,![]() 为严重污染.下面记录了北京市
为严重污染.下面记录了北京市![]() 天的空气质量指数,根据图表,下列结论错误的是( )
天的空气质量指数,根据图表,下列结论错误的是( )

A. 在北京这![]() 天的空气质量中,按平均数来考察,最后
天的空气质量中,按平均数来考察,最后![]() 天的空气质量优于最前面
天的空气质量优于最前面![]() 天的空气质量 B. 在北京这
天的空气质量 B. 在北京这![]() 天的空气质量中,有
天的空气质量中,有![]() 天达到污染程度
天达到污染程度
C. 在北京这![]() 天的空气质量中,12月29日空气质量最好 D. 在北京这
天的空气质量中,12月29日空气质量最好 D. 在北京这![]() 天的空气质量中,达到空气质量优的天数有
天的空气质量中,达到空气质量优的天数有![]() 天
天
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com