
【题目】已知![]() ,
,![]() ,点
,点![]() 满足
满足![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)若直线![]() 过点
过点![]() 且与轨迹
且与轨迹![]() 交于
交于![]() 、
、![]() 两点.
两点.
(i)无论直线![]() 绕点
绕点![]() 怎样转动,在
怎样转动,在![]() 轴上总存在定点
轴上总存在定点![]() ,使
,使![]() 恒成立,求实数
恒成立,求实数![]() 的值.
的值.
(ii)在(i)的条件下,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() (2)(i)
(2)(i)![]() (ii)9
(ii)9
【解析】
(1)利用双曲线的定义及其标准方程即可得出;(2)当直线l的斜率存在时,设直线方程为y=k(x-2),P![]() ,Q
,Q![]() ,与双曲线方程联立消y得
,与双曲线方程联立消y得![]() ,利用根与系数的关系、判别式解出即可得出.(i)利用向量垂直与数量积的关系、根与系数的关系即可得出;(ii)利用点到直线的距离公式、弦长公式、点到直线的距离公式、三角形的面积计算公式即可得出
,利用根与系数的关系、判别式解出即可得出.(i)利用向量垂直与数量积的关系、根与系数的关系即可得出;(ii)利用点到直线的距离公式、弦长公式、点到直线的距离公式、三角形的面积计算公式即可得出
(1)由![]() 知,点P的轨迹E是以F1、F2为焦点的双曲线右支,由
知,点P的轨迹E是以F1、F2为焦点的双曲线右支,由![]() ,故轨迹E的方程为
,故轨迹E的方程为![]()
(2)当直线l的斜率存在时,设直线方程为![]() ,与双曲线方程联立消y得
,与双曲线方程联立消y得![]() ,
,
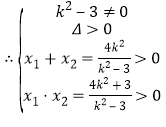 解得k2 >3
解得k2 >3
(i)![]()
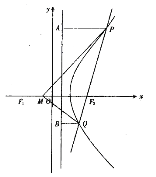
![]() ,
,
故得![]() 对任意的
对任意的![]() 恒成立,
恒成立,
![]() ∴当m =-1时,MP⊥MQ.
∴当m =-1时,MP⊥MQ.
当直线l的斜率不存在时,由![]() 知结论也成立,
知结论也成立,
综上,当m =-1时,MP⊥MQ.
(ii)由(i)知,![]() ,当直线l的斜率存在时,
,当直线l的斜率存在时,
![]() , M点到直线PQ的距离为
, M点到直线PQ的距离为![]() ,则
,则![]()
∴![]()
令![]() ,则
,则![]() ,因为
,因为![]()
所以![]()
当直线l的斜率不存在时,![]()
综上可知![]() ,故
,故![]() 的最小值为9.
的最小值为9.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】对于函数f(x)与g(x)和区间D,如果存在x0∈D,使|f(x0)﹣g(x0)|≤1,则称x0是函数f(x)与g(x)在区间D上的“友好点”.现给出两个函数:
①f(x)=x2 , g(x)=2x﹣2;② ![]() ,g(x)=x+2;
,g(x)=x+2;
③f(x)=e﹣x , ![]() ;④f(x)=lnx,g(x)=x.
;④f(x)=lnx,g(x)=x.
则在区间(0,+∞)上存在唯一“友好点”的是 . (填上所有正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学家欧拉在1765年发现,任意三角形的外心、重心、垂心位于同一条直线上,这条直线称为欧拉线已知![]() 的顶点
的顶点![]() ,若其欧拉线的方程为
,若其欧拉线的方程为![]() ,则顶点
,则顶点![]() 的坐标为( )
的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先把函数y=sin(x+φ)的图象上个点的横坐标缩短为原来的 ![]() (纵坐标不变),再向右平移
(纵坐标不变),再向右平移 ![]() 个单位,所得函数关于y轴对称,则φ的值可以是( )
个单位,所得函数关于y轴对称,则φ的值可以是( )
A.![]()
B.![]()
C.- ![]()
D.- ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机给人们的生活带来便利的同时,也给青少年的成长带来不利的影响,有人沉迷于手机游戏无法自拔,严重影响了自己的学业,某学校随机抽取![]() 个班,调查各班带手机来学校的人数,所得数据的茎叶图如图所示.以组距为
个班,调查各班带手机来学校的人数,所得数据的茎叶图如图所示.以组距为![]() 将数据分组成
将数据分组成![]() ,
,![]() ,…,
,…,![]() ,
,![]() 时,所作的频率分布直方图是( )
时,所作的频率分布直方图是( )

A.  B.
B. 
C. 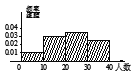 D.
D. 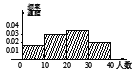
查看答案和解析>>
科目:高中数学 来源: 题型:
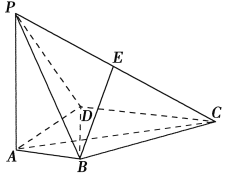
【题目】如图,在四棱锥![]() 中,
中,![]() ⊥底面
⊥底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
(1)(理科生做)证明:![]() ;
;
(文科生做)证明:![]() ;
;
(2)(理科生做)若![]() 为棱
为棱![]() 上一点,满足
上一点,满足![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
(文科生做)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1(a>b>0)的离心率是
=1(a>b>0)的离心率是 ![]() ,过E的右焦点且垂直于椭圆长轴的直线与椭圆交于A,B两点,|AB|=2.
,过E的右焦点且垂直于椭圆长轴的直线与椭圆交于A,B两点,|AB|=2.
(Ⅰ)求椭圆方程;
(Ⅱ)过点P(0, ![]() )的动直线l与椭圆E交于的两点M,N(不是的椭圆顶点),是否存在实数λ,使
)的动直线l与椭圆E交于的两点M,N(不是的椭圆顶点),是否存在实数λ,使 ![]() +λ
+λ ![]() 为定值?若存在,求出λ的值;若不存在,请说明理由.
为定值?若存在,求出λ的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com