
【题目】先把函数y=sin(x+φ)的图象上个点的横坐标缩短为原来的 ![]() (纵坐标不变),再向右平移
(纵坐标不变),再向右平移 ![]() 个单位,所得函数关于y轴对称,则φ的值可以是( )
个单位,所得函数关于y轴对称,则φ的值可以是( )
A.![]()
B.![]()
C.- ![]()
D.- ![]()
【答案】A
【解析】解:把函数y=sin(x+φ)的图象上个点的横坐标缩短为原来的 ![]() (纵坐标不变),可得y=sin(2x+φ)的图象; 再向右平移
(纵坐标不变),可得y=sin(2x+φ)的图象; 再向右平移 ![]() 个单位,可得y=sin(2x﹣
个单位,可得y=sin(2x﹣ ![]() +φ)的图象;
+φ)的图象;
再根据所得函数关于y轴对称,可得﹣ ![]() +φ=kπ+
+φ=kπ+ ![]() ,即φ=kπ+
,即φ=kπ+ ![]() ,k∈Z,令k=﹣1,φ=
,k∈Z,令k=﹣1,φ= ![]() ,
,
故选:A.
【考点精析】本题主要考查了函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1,F2分别为双曲线![]() 的左、右焦点,A1,A2分别为这个双曲线的左、右顶点,P为双曲线右支上的任意一点.求证:以A1A2为直径的圆既与以PF2为直径的圆外切,又与以PF1为直径的圆内切.
的左、右焦点,A1,A2分别为这个双曲线的左、右顶点,P为双曲线右支上的任意一点.求证:以A1A2为直径的圆既与以PF2为直径的圆外切,又与以PF1为直径的圆内切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,
中, ![]() 面
面![]() ,
, ![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() ,平面
,平面![]() 与
与![]() 交于点
交于点![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的正切值为__________.
所成角的正切值为__________.
【答案】![]()
【解析】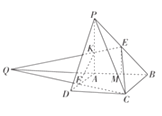
延长![]() 交
交![]() 的延长线与点Q,连接QE交PA于点K,设QA=x,
的延长线与点Q,连接QE交PA于点K,设QA=x,
由![]() ,得
,得![]() ,则
,则![]() ,所以
,所以![]() .
.
取![]() 的中点为M,连接EM,则
的中点为M,连接EM,则![]() ,
,
所以![]() ,则
,则![]() ,所以AK=
,所以AK=![]() .
.
由AD//BC,得异面直线![]() 与
与![]() 所成角即为
所成角即为![]() ,
,
则异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() .
.
【题型】填空题
【结束】
17
【题目】在极坐标系中,极点为![]() ,已知曲线
,已知曲线![]() :
: ![]() 与曲线
与曲线![]() :
: ![]() 交于不同的两点
交于不同的两点![]() ,
, ![]() .
.
(1)求![]() 的值;
的值;
(2)求过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,棱柱ABCD﹣A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC= ![]() ,BC=BB1=2.
,BC=BB1=2. 
(Ⅰ)求证:AC⊥平面ABB1A1;
(Ⅱ)求二面角A﹣C1D﹣C的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,点
,点![]() 满足
满足![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)若直线![]() 过点
过点![]() 且与轨迹
且与轨迹![]() 交于
交于![]() 、
、![]() 两点.
两点.
(i)无论直线![]() 绕点
绕点![]() 怎样转动,在
怎样转动,在![]() 轴上总存在定点
轴上总存在定点![]() ,使
,使![]() 恒成立,求实数
恒成立,求实数![]() 的值.
的值.
(ii)在(i)的条件下,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①命题:x∈(0,2),3x>x3的否定是:x∈(0,2),3x≤x3;
②若f(x)=2x﹣2﹣x , 则x∈R,f(﹣x)=﹣f(x);
③若f(x)=x+ ![]() ,则x0∈(0,+∞),f(x0)=1;
,则x0∈(0,+∞),f(x0)=1;
④等差数列{an}的前n项和为Sn , 若a4=3,则S7=21;
⑤在△ABC中,若A>B,则sinA>sinB.
其中真命题是 . (只填写序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)= ![]() (x>0),计算观察以下格式: f1(x)=f(x),f2(x)=f(f1(x)),f3(x)=f(f2(x)),f4(x)=f(f3(x)),…
(x>0),计算观察以下格式: f1(x)=f(x),f2(x)=f(f1(x)),f3(x)=f(f2(x)),f4(x)=f(f3(x)),…
根据以上事实得到当n∈N*时,fn(1)= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com