
【题目】某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场没销售一台空调器可获利500元,若供大于求,则每台多余的空调器需交保管费100元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润200元.
(Ⅰ)若该商场周初购进20台空调器,求当周的利润(单位:元)关于当周需求量![]() (单位:台,
(单位:台,![]() )的函数解析式
)的函数解析式![]() ;
;
(Ⅱ)该商场记录了去年夏天(共10周)空调器需求量(单位:台),整理得下表:

以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,![]() 表示当周的利润(单位:元),求
表示当周的利润(单位:元),求![]() 的分布及数学期望.
的分布及数学期望.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】如图1,在高为2的梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() ,
, ![]() ,垂足分别为
,垂足分别为![]() 、
、![]() 。已知
。已知![]() ,将梯形
,将梯形![]() 沿
沿![]() 、
、![]() 同侧折起,得空间几何体
同侧折起,得空间几何体![]() ,如图2。
,如图2。

(1)若![]() ,证明:
,证明: ![]() ;
;
(2)若![]() ,证明:
,证明: ![]() ;
;
(3)在(1),(2)的条件下,求三棱锥![]() 的体积。
的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三共有2000名学生参加广安市联考,现随机抽取100名学生的成绩(单位:分),并列成如下表所示的频数分布表:
组别 |
|
|
|
|
|
|
频数 | 6 | 18 | 28 | 26 | 17 | 5 |
(1)试估计该年级成绩![]() 分的学生人数;
分的学生人数;
(2)已知样本中成绩在![]() 中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年天猫五一活动结束后,某地区研究人员为了研究该地区在五一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得概率分布直方图如图所示:记年龄在![]() ,
, ![]() ,
, ![]() 对应的小矩形的面积分别是
对应的小矩形的面积分别是![]() ,且
,且![]() .
.
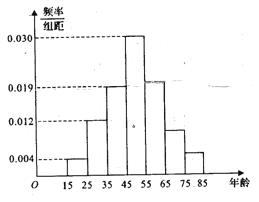
(1)以频率作为概率,若该地区五一消费超过3000元的有30000人,试估计该地区在五一活动中消费超过3000元且年龄在![]() 的人数;
的人数;
(2)计算在五一活动中消费超过3000元的消费者的平均年龄;
(3)若按照分层抽样,从年龄在![]() ,
, ![]() 的人群中共抽取7人,再从这7人中随机抽取2人作深入调查,求至少有1人的年龄在
的人群中共抽取7人,再从这7人中随机抽取2人作深入调查,求至少有1人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为Sn,点
的前n项和为Sn,点![]() 在直线
在直线![]() 上,数列
上,数列![]() 为等差数列,且
为等差数列,且![]() ,前9项和为153.
,前9项和为153.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,求使不等式
,求使不等式![]() 对一切的
对一切的![]() 都成立的最大整数k.
都成立的最大整数k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(2,0),且圆C:x2+y2﹣6x+4y+4=0.
(Ⅰ)当直线![]() 过点P且与圆心C的距离为1时,求直线
过点P且与圆心C的距离为1时,求直线![]() 的方程;
的方程;
(Ⅱ)设过点P的直线与圆C交于A、B两点,若|AB|=4,求以线段AB为直径的圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com