
ЎѕМвДїЎїДіРЎРНЖуТµјЧІъЖ·ЙъІъµДН¶ИліЙ±ѕ![]() ЈЁµҐО»ЈєНтФЄЈ©УлІъЖ·ПъКЫКХИл
ЈЁµҐО»ЈєНтФЄЈ©УлІъЖ·ПъКЫКХИл![]() ЈЁµҐО»ЈєНтФЄЈ©ґжФЪЅПєГµДПЯРФ№ШПµЈ¬ПВ±нјЗВјБЛЧоЅь5ґОІъЖ·µДПа№ШКэѕЭ.
ЈЁµҐО»ЈєНтФЄЈ©ґжФЪЅПєГµДПЯРФ№ШПµЈ¬ПВ±нјЗВјБЛЧоЅь5ґОІъЖ·µДПа№ШКэѕЭ.
| 7 | 10 | 11 | 15 | 17 |
| 19 | 22 | 25 | 30 | 34 |
ЈЁ1Ј©Зу![]() №ШУЪ
№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМЈ»
µДПЯРФ»Ш№й·ЅіМЈ»
ЈЁ2Ј©ёщѕЭЈЁ1Ј©ЦРµД»Ш№й·ЅіМЈ¬ЕР¶ПёГЖуТµјЧІъЖ·Н¶ИліЙ±ѕ20НтФЄµДГ«АыВКёьґу»№КЗН¶ИліЙ±ѕ24НтФЄµДГ«АыВКёьґуЈЁ![]() Ј©Јї
Ј©Јї
Па№Ш№«КЅЈє 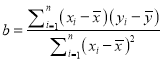
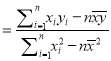 Ј¬
Ј¬ ![]() .
.
Ўѕґр°ёЎїЈЁ1Ј©![]() .ЈЁ2Ј©Н¶ИліЙ±ѕ20НтФЄµДГ«АыВКёьґу.
.ЈЁ2Ј©Н¶ИліЙ±ѕ20НтФЄµДГ«АыВКёьґу.
ЎѕЅвОцЎїКФМв·ЦОцЈєЈЁ1Ј©Уɻع鹫ʽЈ¬ЅвµГПЯРФ»Ш№й·ЅіМОЄ![]() Ј»ЈЁ2Ј©µ±
Ј»ЈЁ2Ј©µ±![]() К±Ј¬
К±Ј¬ ![]() Ј¬¶ФУ¦µДГ«АыВКОЄ
Ј¬¶ФУ¦µДГ«АыВКОЄ![]() Ј¬µ±
Ј¬µ±![]() К±Ј¬
К±Ј¬ ![]() Ј¬¶ФУ¦µДГ«АыВКОЄ
Ј¬¶ФУ¦µДГ«АыВКОЄ![]() Ј¬№КН¶ИліЙ±ѕ20НтФЄµДГ«АыВКёьґуЎЈ
Ј¬№КН¶ИліЙ±ѕ20НтФЄµДГ«АыВКёьґуЎЈ
КФМвЅвОцЈє
ЈЁ1Ј©![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬
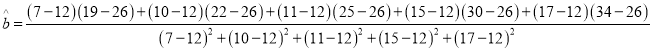
![]() Ј¬
Ј¬ ![]() Ј¬№К
Ј¬№К![]() №ШУЪ
№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМОЄ
µДПЯРФ»Ш№й·ЅіМОЄ![]() .
.
ЈЁ2Ј©µ±![]() К±Ј¬
К±Ј¬ ![]() Ј¬¶ФУ¦µДГ«АыВКОЄ
Ј¬¶ФУ¦µДГ«АыВКОЄ![]() Ј¬
Ј¬
µ±![]() К±Ј¬
К±Ј¬ ![]() Ј¬¶ФУ¦µДГ«АыВКОЄ
Ј¬¶ФУ¦µДГ«АыВКОЄ![]() Ј¬
Ј¬
№КН¶ИліЙ±ѕ20НтФЄµДГ«АыВКёьґу.
ЎѕМвРНЎїЅвґрМв
ЎѕЅбКшЎї
21
ЎѕМвДїЎїТСЦЄНЦФІ![]() µДТ»ёцЅ№µгОЄ
µДТ»ёцЅ№µгОЄ![]() .ЙиНЦФІ
.ЙиНЦФІ![]() µДЅ№µгЗЎОЄНЦФІ
µДЅ№µгЗЎОЄНЦФІ![]() ¶МЦбµД¶ҐµгЈ¬ЗТНЦФІ
¶МЦбµД¶ҐµгЈ¬ЗТНЦФІ![]() №эµг
№эµг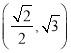 .
.
ЈЁ1Ј©Зу![]() µД·ЅіМј°АлРДВКЈ»
µД·ЅіМј°АлРДВКЈ»
ЈЁ2Ј©ИфЦ±ПЯ![]() УлНЦФІ
УлНЦФІ![]() Ѕ»УЪ
Ѕ»УЪ![]() БЅµгЈ¬Зу
БЅµгЈ¬Зу![]() .
.

| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї¶ФУЪєЇКэ![]() УРТФПВЛµ·ЁЈє
УРТФПВЛµ·ЁЈє
ўЩ![]() КЗ
КЗ![]() µДј«Цµµг.
µДј«Цµµг.
ўЪµ±![]() К±Ј¬
К±Ј¬ ![]() ФЪ
ФЪ![]() ЙПКЗјхєЇКэ.
ЙПКЗјхєЇКэ.
ўЫ![]() µДНјПсУл
µДНјПсУл![]() ґ¦µДЗРПЯ±ШПаЅ»УЪБнТ»µг.
ґ¦µДЗРПЯ±ШПаЅ»УЪБнТ»µг.
ўЬµ±![]() К±Ј¬
К±Ј¬ ![]() ФЪ
ФЪ![]() ЙПКЗјхєЇКэ.
ЙПКЗјхєЇКэ.
ЖдЦРЛµ·ЁХэИ·µДРтєЕКЗ_______________.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() КЗ¶ЁТеФЪ
КЗ¶ЁТеФЪ![]() ЙПµДЕјєЇКэЈ¬ЗТµ±
ЙПµДЕјєЇКэЈ¬ЗТµ±![]() К±Ј¬
К±Ј¬![]() .
.

ЈЁ1Ј©ТС»іцєЇКэ![]() ФЪ
ФЪ![]() ЦбЧуІаµДНјПсЈ¬ИзНјЛщКѕЈ¬ЗлІ№іцНкХыєЇКэ
ЦбЧуІаµДНјПсЈ¬ИзНјЛщКѕЈ¬ЗлІ№іцНкХыєЇКэ![]() µДНјПсЈ¬ІўёщѕЭНјПсРґіцєЇКэ
µДНјПсЈ¬ІўёщѕЭНјПсРґіцєЇКэ![]() µДФцЗшјдЈ»
µДФцЗшјдЈ»
ўЖРґіцєЇКэ![]() µДЅвОцКЅєНЦµУт.
µДЅвОцКЅєНЦµУт.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЅ«єЇКэ ![]() µДНјПуПтЧуЖЅТЖ
µДНјПуПтЧуЖЅТЖ ![]() ёцµҐО»Ј¬ФЩПтПВЖЅТЖ4ёцµҐО»Ј¬µГµЅєЇКэgЈЁxЈ©µДНјПуЈ¬ФтєЇКэfЈЁxЈ©µДНјПуУлєЇКэgЈЁxЈ©µДНјПуЈЁ Ј©
ёцµҐО»Ј¬ФЩПтПВЖЅТЖ4ёцµҐО»Ј¬µГµЅєЇКэgЈЁxЈ©µДНјПуЈ¬ФтєЇКэfЈЁxЈ©µДНјПуУлєЇКэgЈЁxЈ©µДНјПуЈЁ Ј©
A.№ШУЪµгЈЁ©Ѓ2Ј¬0Ј©¶ФіЖ
B.№ШУЪµгЈЁ0Ј¬©Ѓ2Ј©¶ФіЖ
C.№ШУЪЦ±ПЯx=©Ѓ2¶ФіЖ
D.№ШУЪЦ±ПЯx=0¶ФіЖ
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪИэАвЧ¶A©ЃBCDЦРЈ¬ІаАвABЈ¬ACЈ¬ADБЅБЅґ№Ц±Ј¬ЎчABCЎўЎчACDЎўЎчABDµДГж»э·Ц±рОЄ ![]() Ўў
Ўў ![]() Ўў2
Ўў2 ![]() Ј¬ФтИэАвЧ¶A©ЃBCDµДНвЅУЗтµДМе»эОЄ Ј®
Ј¬ФтИэАвЧ¶A©ЃBCDµДНвЅУЗтµДМе»эОЄ Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() Ј¬ЗТ
Ј¬ЗТ![]() Ј¬Фт
Ј¬Фт ![]() µДЦµЈЁ Ј©
µДЦµЈЁ Ј©
A. єгОЄХэКэ B. єгµИУЪБг
C. єгОЄёєКэ D. їЙДЬґуУЪБгЈ¬ТІїЙДЬРЎУЪБг
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДіµШЗш10ГыЅЎїµ¶щНЇН··ўєНСЄТєЦРµДОшє¬Бї(µҐО»Јє¦Мg/ml)ИзПВ±нЛщКѕЈє
СЄОшx | 74 | 66 | 88 | 69 | 91 | 73 | 66 | 96 | 58 | 73 |
·ўОшy | 13 | 10 | 13 | 11 | 16 | 9 | 7 | 14 | 5 | 10 |
(1)»іцЙўµгНјЈ»
(2)Зу»Ш№й·ЅіМЈ»
(3)ИфДіГыЅЎїµ¶щНЇµДСЄТєЦРµДОшє¬БїОЄ94 ¦Мg/mlЈ¬Ф¤ІвЛыµД·ўОшє¬БїЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄФІ![]() Јє
Јє ![]() ЈЁЖдЦР
ЈЁЖдЦР![]() ОЄФІРДЈ©ЙПµДГїТ»µгєбЧш±кІ»±дЈ¬ЧЭЧш±к±дОЄФАґµДТ»°лЈ¬µГµЅЗъПЯ
ОЄФІРДЈ©ЙПµДГїТ»µгєбЧш±кІ»±дЈ¬ЧЭЧш±к±дОЄФАґµДТ»°лЈ¬µГµЅЗъПЯ![]() .
.
ЈЁ1Ј©ЗуЗъПЯ![]() µД·ЅіМЈ»
µД·ЅіМЈ»
ЈЁ2Ј©Ифµг![]() ОЄЗъПЯ
ОЄЗъПЯ![]() ЙПТ»µгЈ¬№эµг
ЙПТ»µгЈ¬№эµг![]() ЧчЗъПЯ
ЧчЗъПЯ![]() µДЗРПЯЅ»ФІ
µДЗРПЯЅ»ФІ![]() УЪІ»Н¬µДБЅµг
УЪІ»Н¬µДБЅµг![]() ЈЁЖдЦР
ЈЁЖдЦР![]() ФЪ
ФЪ![]() µДУТІаЈ©Ј¬ТСЦЄµг
µДУТІаЈ©Ј¬ТСЦЄµг![]() .ЗуЛД±ЯРО
.ЗуЛД±ЯРО![]() Гж»эµДЧоґуЦµ.
Гж»эµДЧоґуЦµ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬Хэ·ЅМе![]() µДАві¤ОЄ
µДАві¤ОЄ![]() Ј¬
Ј¬ ![]() ОЄ
ОЄ![]() µДЦРµгЈ¬
µДЦРµгЈ¬ ![]() ОЄПЯ¶О
ОЄПЯ¶О![]() ЙПµД¶ЇµгЈ¬№эµг
ЙПµД¶ЇµгЈ¬№эµг![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() µДЖЅГжЅШёГХэ·ЅМеЛщµГµДЅШГжОЄ
µДЖЅГжЅШёГХэ·ЅМеЛщµГµДЅШГжОЄ![]() Ј¬ФтПВБРГьМвХэИ·µДКЗ__________ЈЁРґіцЛщУРХэИ·ГьМвµД±аєЕЈ©.
Ј¬ФтПВБРГьМвХэИ·µДКЗ__________ЈЁРґіцЛщУРХэИ·ГьМвµД±аєЕЈ©.

ўЩµ±![]() К±Ј¬
К±Ј¬ ![]() ОЄЛД±ЯРОЈ»ўЪµ±
ОЄЛД±ЯРОЈ»ўЪµ±![]() К±Ј¬
К±Ј¬ ![]() ОЄµИСьМЭРОЈ»
ОЄµИСьМЭРОЈ»
ўЫµ±![]() К±Ј¬
К±Ј¬ ![]() Ул
Ул![]() µДЅ»µг
µДЅ»µг![]() ВъЧг
ВъЧг![]() Ј»
Ј»
ўЬµ±![]() К±Ј¬
К±Ј¬ ![]() ОЄОе±ЯРОЈ»
ОЄОе±ЯРОЈ»
ўЭµ±![]() К±Ј¬
К±Ј¬ ![]() µДГж»эОЄ
µДГж»эОЄ![]() .
.
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com