
已知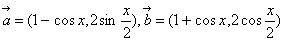
(1)若 求
求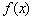 的表达式.
的表达式.
(2)若函数 和函数
和函数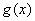 的图象关于原点对称,求
的图象关于原点对称,求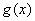 的解析式.
的解析式.
(3)若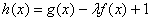 在
在 上是增函数,求实数l的取值范围.
上是增函数,求实数l的取值范围.
|
t(时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y(米) |
1.0 |
1.4 |
1.0 |
0.6 |
1.0 |
1.4 |
0.9 |
0.4 |
1.0 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 学生的编号i | 1 | 2 | 3 | 4 | 5 |
| 数学xi | 80 | 75 | 70 | 65 | 60 |
| 物理yi | 70 | 66 | 68 | 64 | 62 |
| ? |
| y |
| |||||||
|
. |
| y |
. |
| x |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
| x | 2 i |
| 5 |
 |
| i=1 |
| ? |
| y |
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(x) |
| x |
| f(x) |
| x2 |
| x | a | b | c | a+b+c |
| f(x) | d | d | t | 4 |
查看答案和解析>>
科目:高中数学 来源:2011届河北省正定中学高三第四次月考数学理卷 题型:解答题
(本小题满分12分)把正奇数列 中的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表.设
中的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表.设 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行,从左向右数第
行,从左向右数第 个数.
个数.
(1)若 ,求
,求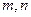 的值;
的值;
(2)已知函数 的反函数为
的反函数为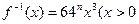 ,
, ),若记三角形数表中从上往下数第
),若记三角形数表中从上往下数第 行各数的和为
行各数的和为 .
.
①求数列 的前
的前 项的和
项的和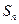 .
.
②令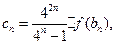 设
设 的前
的前 项之积为
项之积为 ,求证:
,求证:

查看答案和解析>>
科目:高中数学 来源:2011-2012学年黑龙江哈尔滨市高三第三次模拟考试理科数学试卷(解析版) 题型:解答题
已知 .
.
(1)求 的单调区间;
的单调区间;
(2)证明:当 时,
时, 恒成立;
恒成立;
(3)任取两个不相等的正数 ,且
,且 ,若存在
,若存在 使
使 成立,证明:
成立,证明: .
.
【解析】(1)g(x)=lnx+ ,
, =
=
 (1’)
(1’)
当k 0时,
0时, >0,所以函数g(x)的增区间为(0,+
>0,所以函数g(x)的增区间为(0,+ ),无减区间;
),无减区间;
当k>0时, >0,得x>k;
>0,得x>k; <0,得0<x<k∴增区间(k,+
<0,得0<x<k∴增区间(k,+ )减区间为(0,k)(3’)
)减区间为(0,k)(3’)
(2)设h(x)=xlnx-2x+e(x 1)令
1)令 = lnx-1=0得x=e, 当x变化时,h(x),
= lnx-1=0得x=e, 当x变化时,h(x), 的变化情况如表
的变化情况如表
|
x |
1 |
(1,e) |
e |
(e,+ |
|
|
|
- |
0 |
+ |
|
h(x) |
e-2 |
|
0 |
↗ |
所以h(x) 0, ∴f(x)
0, ∴f(x) 2x-e
(5’)
2x-e
(5’)
设G(x)=lnx- (x
(x 1)
1)  =
= =
=
 0,当且仅当x=1时,
0,当且仅当x=1时, =0所以G(x) 为减函数, 所以G(x)
=0所以G(x) 为减函数, 所以G(x)  G(1)=0, 所以lnx-
G(1)=0, 所以lnx-
 0所以xlnx
0所以xlnx
 (x
(x 1)成立,所以f(x)
1)成立,所以f(x) 
 ,综上,当x
,综上,当x 1时, 2x-e
1时, 2x-e f(x)
f(x)
 恒成立.
恒成立.
(3) ∵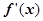 =lnx+1∴lnx0+1=
=lnx+1∴lnx0+1= =
= ∴lnx0=
∴lnx0=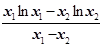 -1
∴lnx0 –lnx
-1
∴lnx0 –lnx =
= -1–lnx
-1–lnx =
= =
= =
= (10’) 设H(t)=lnt+1-t(0<t<1),
(10’) 设H(t)=lnt+1-t(0<t<1),
 =
= =
=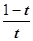 >0(0<t<1), 所以H(t) 在(0,1)上是增函数,并且H(t)在t=1处有意义, 所以H(t)
<H(1)=0∵
>0(0<t<1), 所以H(t) 在(0,1)上是增函数,并且H(t)在t=1处有意义, 所以H(t)
<H(1)=0∵ ∴
∴ =
=
∴lnx0 –lnx >0, ∴x0 >x
>0, ∴x0 >x
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河北省高三第四次月考数学理卷 题型:解答题
(本小题满分12分)把正奇数列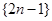 中的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表.设
中的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表.设 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行,从左向右数第
行,从左向右数第 个数.
个数.
(1)若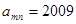 ,求
,求 的值;
的值;
(2)已知函数 的反函数为
的反函数为 ,
, ),若记三角形数表中从上往下数第
),若记三角形数表中从上往下数第 行各数的和为
行各数的和为 .
.
①求数列 的前
的前 项的和
项的和 .
.
②令 设
设 的前
的前 项之积为
项之积为
 ,求证:
,求证:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com