
����Ŀ��ȥ�ꡰʮһ���ڼ䣬�������ٹ�·�����϶࣮ij���鹫˾�������շ�վ��7������С�������а����շ�վ���Ⱥ�˳��ÿ���50���ͳ�ȡһ���ij���������ȡ40���������г������飬��������ij�θ��ٹ�·�ij��٣�![]() ���ֳ����Σ�
���ֳ����Σ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
�õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��

��I�����鹫˾�ڳ���ʱ�õ��������ֳ���������
��II������40��С���������ٵ���������λ���Ĺ���ֵ��
��III��������40��������![]() ��С�������������ȡ2����������2�������ٶ���
��С�������������ȡ2����������2�������ٶ���![]() �ĸ��ʣ�
�ĸ��ʣ�
���𰸡���I��ϵͳ��������II�������Ĺ���ֵΪ![]() ����λ���Ĺ���ֵΪ
����λ���Ĺ���ֵΪ![]() ����III��
����III��![]() .
.
��������
���⣨I��������ÿ���![]() ���ͳ�ȡһ����Ҳ����˵��ȡ�����������ȣ�����ϵͳ�����Ĺ���II��������ָ����Ƶ����ߵ�������Ƶ�ʷֲ�ֱ��ͼ���ø�����е������������ݾ�����Ƶ�ʷֲ�ֱ��ͼ��Ƶ��Ϊ
���ͳ�ȡһ����Ҳ����˵��ȡ�����������ȣ�����ϵͳ�����Ĺ���II��������ָ����Ƶ����ߵ�������Ƶ�ʷֲ�ֱ��ͼ���ø�����е������������ݾ�����Ƶ�ʷֲ�ֱ��ͼ��Ƶ��Ϊ![]() �ķֽ�㣬���ݸ������ε��������⼴�ɣ���III�������㳵����
�ķֽ�㣬���ݸ������ε��������⼴�ɣ���III�������㳵����![]() �Ĺ���
�Ĺ���![]() �������г�����
�����������![]() ����
����![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��������
��������![]() ����
����![]() ������Ϊ
������Ϊ![]() ��
��![]() ���оٳ���
���оٳ���![]() �������г�ȡ
�������г�ȡ![]() ��������ȡ�����ҳ������
��������ȡ�����ҳ������![]() �������ٶ���
�������ٶ���![]() ��ȡ�������ȼ���Ҫ��ĸ���.
��ȡ�������ȼ���Ҫ��ĸ���.
�����������I��ϵͳ������
��II�������Ĺ���ֵΪ��ߵľ��ε��е㣬�������Ĺ���ֵΪ![]() ��
��
����ͼ��֪����λ��Ӧ����![]() ֮�䣬��Ϊ
֮�䣬��Ϊ![]() ��
��
��![]() ��
��![]() ��
��
����λ���Ĺ���ֵΪ![]() ��
��
��III����![]() ������������
�����У�������![]() �Ĺ���
����![]() ����
����
�������![]() ����
����![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��
������![]() ����
����![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��
���ӳ�����![]() ����
����![]() �������������ȡ
�������������ȡ![]() ���Ŀ��ܽ���У�
���Ŀ��ܽ���У�
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �ֲ�ͬ�Ľ����
�ֲ�ͬ�Ľ����
���г����![]() �������ٶ���
�������ٶ���![]() �Ľ����
�Ľ����![]() �֣�
�֣�
��Ϊ�鵽ÿ�ֽ�����ǵȿ��ܵģ�
���Դ���![]() ��������
��������![]() �������������ȡ
�������������ȡ![]() ���������
���������![]() �������ٶ���
�������ٶ���![]() �ĸ���Ϊ
�ĸ���Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ���ڶ���P��x��y����ԲF��x2+��y��1��2=1��Բ��F�ľ��������ֱ��y=��2�ľ���С1��
��1����P�Ĺ켣���̣�
��2�����P�Ĺ켣Ϊ����E������F��ֱ��l��б��Ϊk��ֱ��l������E��A��B���㣬��ԲF��C��D���㣨A��C�������ڣ���
���� ![]() =t
=t ![]() ����t��[1��2]ʱ����k��ȡֵ��Χ��
����t��[1��2]ʱ����k��ȡֵ��Χ��
�ڹ�A��B����ֱ�������E������l1 �� l2 �� �����߽��ڵ�N�����ACN���BDN���֮������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AB��CD��AD��BC��AD=3��BC=2AB=2��E��F�ֱ���BC��AD�ϣ�EF��AB���ֽ��ı���ABEF��EF����ʹƽ��ABEF��ƽ��EFDC��
������BE= ![]() �����۵�����߶�AD���Ƿ����һ��P����
�����۵�����߶�AD���Ƿ����һ��P���� ![]() ��ʹ��CP��ƽ��ABEF�������ڣ�����˵�ֵ���������ڣ�˵�����ɣ�
��ʹ��CP��ƽ��ABEF�������ڣ�����˵�ֵ���������ڣ�˵�����ɣ�
����������A��CDF����������ֵ�������ʱ�����E��AC��F������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������E��y2=2px��p��0��������x�ύ�ڵ�K������K��Բ��x��5��2+y2=9���������ߣ��е�ΪM��N��|MN|=3 ![]()
��1����������E�ķ��̣�
��2����A��B��������E�Ϸֱ�λ��x��������������㣬�� ![]() ������OΪ����ԭ�㣩��
������OΪ����ԭ�㣩��
����֤��ֱ��AB�ع����㣬������ö���Q�����ꣻ
�ڹ���Q��AB�Ĵ����������߽���G��D���㣬���ı���AGBD�������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=2 ![]() sin
sin ![]() cos
cos ![]() ��2sin2
��2sin2 ![]() ���أ�0������С������Ϊ3�У�
���أ�0������С������Ϊ3�У�
��I������f��x���ĵ����������䣻
�����ڡ�ABC�У�a��b��c�ֱ�Ϊ��A��B��C���Եıߣ�a��b��c�� ![]() a=2csinA������f��
a=2csinA������f�� ![]() A+
A+ ![]() ��=
��= ![]() ����cosB��ֵ��
����cosB��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC����x��2��2+��y��3��2=16��ֱ��l����m+2��x+��3m+1��y=15m+10��m��R����
��1��֤��������mȡʲôʵ����ֱ��l��ԲC���ཻ��
��2����ֱ��l��ԲC�صõ��ҳ�����̳��ȼ���ʱ��ֱ�߷��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����ABCD��A1B1C1D1�У�AA1=AD=a��EΪCD������һ�㣮
��I����֤��B1E��AD1��
������CD= ![]() a���Ƿ����������E�㣬ʹ��AD1��ƽ��B1AE��45��Ľǣ�˵�����ɣ�
a���Ƿ����������E�㣬ʹ��AD1��ƽ��B1AE��45��Ľǣ�˵�����ɣ�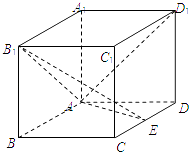
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x�IJ���ʽ��mx����m+1������x��2��>0��m![]() R���Ľ⼯Ϊ����P
R���Ľ⼯Ϊ����P
��I����m>0ʱ����P��
��II����{![]() }
}![]() P����m��ȡֵ��Χ.
P����m��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ,��x = -1ʱȡ�ü���ֵ7����x = 3ʱȡ�ü�Сֵ��
,��x = -1ʱȡ�ü���ֵ7����x = 3ʱȡ�ü�Сֵ��
��1����a,b��ֵ��
��2����f(x)�ļ�Сֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com