
【题目】已知点![]() ,
,![]() 是函数
是函数![]() 的图像上任意不同的两点,依据图像可知,线段
的图像上任意不同的两点,依据图像可知,线段![]() 总是位于
总是位于![]() 两点之间函数图像的上方,因此有结论
两点之间函数图像的上方,因此有结论![]() 成立,运用类比的思想方法可知,若点
成立,运用类比的思想方法可知,若点![]() ,
,![]() 是函数
是函数![]() 的图像上任意不同的两点,则类似地有_________成立.
的图像上任意不同的两点,则类似地有_________成立.
科目:高中数学 来源: 题型:
【题目】大豆是我国主要的农作物之一,因此,大豆在农业发展中占有重要的地位,随着农业技术的不断发展,为了使大豆得到更好的种植,就要进行超级种培育研究.某种植基地培育的“超级豆”种子进行种植测试:选择一块营养均衡的可种植![]() 株的实验田地,每株放入三粒“超级豆”种子,且至少要有一粒种子发芽这株豆苗就能有效成活,每株豆成活苗可以收成大豆
株的实验田地,每株放入三粒“超级豆”种子,且至少要有一粒种子发芽这株豆苗就能有效成活,每株豆成活苗可以收成大豆![]() .已知每粒豆苗种子成活的概率为
.已知每粒豆苗种子成活的概率为![]() (假设种子之间及外部条件一致,发芽相互没有影响).
(假设种子之间及外部条件一致,发芽相互没有影响).
(Ⅰ)求恰好有3株成活的概率;
(Ⅱ)记成活的豆苗株数为![]() ,收成为
,收成为![]() ,求随机变量
,求随机变量![]() 分布列及
分布列及![]() 数学期望
数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC![]() 中,侧面
中,侧面![]() 是矩形,∠BAC=90°,
是矩形,∠BAC=90°,![]() ⊥BC,
⊥BC,![]() =AC=2AB=4,且
=AC=2AB=4,且![]() ⊥
⊥![]() .
.

(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)设D是![]() 的中点,判断并证明在线段
的中点,判断并证明在线段![]() 上是否存在点E,使得DE∥平面
上是否存在点E,使得DE∥平面![]() .若存在,求二面角E
.若存在,求二面角E![]() B的余弦值.
B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 具有性质:若
具有性质:若![]() 、
、![]() 是双曲线左、右顶点,
是双曲线左、右顶点,![]() 为双曲线上一点,且
为双曲线上一点,且![]() 在第一象限.记直线
在第一象限.记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,那么
,那么![]() 与
与![]() 之积是与点
之积是与点![]() 位置无关的定值.
位置无关的定值.
(1)试对椭圆![]() ,类比写出类似的性质(不改变原有命题的字母次序),并加以证明.
,类比写出类似的性质(不改变原有命题的字母次序),并加以证明.
(2)若椭圆![]() 的左焦点
的左焦点![]() ,右准线为
,右准线为![]() ,在(1)的条件下,当
,在(1)的条件下,当![]() 取得最小值时,求
取得最小值时,求![]() 的垂心
的垂心![]() 到
到![]() 轴的距离.
轴的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
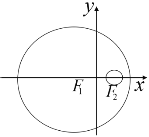
【题目】如图,已知圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,若动圆
,若动圆![]() 与圆
与圆![]() 内切,与圆
内切,与圆![]() 外切.
外切.
(Ⅰ)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过直线![]() 上的点
上的点![]() 作圆
作圆![]() 的两条切线,设切点分别是
的两条切线,设切点分别是![]() ,
,![]() ,若直线
,若直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 世纪
世纪![]() 年代,里克特(C.F.Richter)制定了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大.这就是我们常说的里氏震级
年代,里克特(C.F.Richter)制定了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大.这就是我们常说的里氏震级![]() ,其计算公式为:
,其计算公式为:![]() ,其中,
,其中,![]() 是被测地震的最大振幅,
是被测地震的最大振幅,![]() 是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差).(以下数据供参考:
是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差).(以下数据供参考:![]() ,
,![]() ,
,![]() )
)
(1)根据中国地震台网测定,![]() 年
年![]() 月
月![]() 日
日![]() 时
时![]() 分,新疆巴音郭楞蒙古自治州若羌县发生地震,一个距离震中
分,新疆巴音郭楞蒙古自治州若羌县发生地震,一个距离震中![]() 千米的测震仪记录的地震最大振幅是
千米的测震仪记录的地震最大振幅是![]() ,此时标准地震的振幅是
,此时标准地震的振幅是![]() ,计算这次地震的震级(精确到
,计算这次地震的震级(精确到![]() );
);
(2)![]() 年
年![]() 月
月![]() 日
日![]() 时
时![]() 分
分![]() 秒在我国四川省汶川地区发生特大地震,根据中华人民共和国地震局的数据,此次地震的里氏震级达
秒在我国四川省汶川地区发生特大地震,根据中华人民共和国地震局的数据,此次地震的里氏震级达![]() ,地震烈度达到
,地震烈度达到![]() 度.此次地震的地震波已确认共环绕了地球
度.此次地震的地震波已确认共环绕了地球![]() 圈.地震波及大半个中国及亚洲多个国家和地区,北至辽宁,东至上海,南至香港、澳门、泰国、越南,西至巴基斯坦均有震感.请计算汶川地震的最大振幅是
圈.地震波及大半个中国及亚洲多个国家和地区,北至辽宁,东至上海,南至香港、澳门、泰国、越南,西至巴基斯坦均有震感.请计算汶川地震的最大振幅是![]() 级地震的最大振幅的多少倍?
级地震的最大振幅的多少倍?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,且椭圆的短轴长为2.
,且椭圆的短轴长为2.
(1)球椭圆的标准方程;
(2)已知直线![]() 过右焦点
过右焦点![]() ,且它们的斜率乘积为
,且它们的斜率乘积为![]() ,设
,设![]() 分别与椭圆交于点
分别与椭圆交于点![]() 和
和![]() .
.
①求![]() 的值;
的值;
②设![]() 的中点
的中点![]() ,
,![]() 的中点为,求
的中点为,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】20名高二学生某次数学考试成绩(单位:分)的频率分布直方图如图:
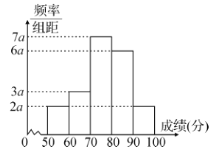
(1)求频率分布直方图中![]() 的值;
的值;
(2)分别求出成绩落在![]() 与
与![]() 中的学生人数;
中的学生人数;
(3)从成绩在![]() 的学生中任选2人,求此2人的成绩都在
的学生中任选2人,求此2人的成绩都在![]() 中的概率.
中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com