
【题目】根据下列算法语句,将输出的A值依次记为a1,a2,…,an,…,a2015;已知函数f(x)=a2sin(ωx+φ)(ω>0,|φ|<![]() )的最小正周期是a1,且函数
)的最小正周期是a1,且函数![]() 的图象关于直线x=
的图象关于直线x=![]() 对称。
对称。

(Ⅰ)求函数![]() 表达式;
表达式;
(Ⅱ)已知△ABC中三边a,b,c对应角A,B,C,a=4,b=4![]() ,∠A=30°,求
,∠A=30°,求![]() 。
。
【答案】(Ⅰ)f(x)=4sin(2πx+![]() )(Ⅱ)4sin(
)(Ⅱ)4sin(![]() +
+![]() )或4sin(
)或4sin(![]() +
+![]() )
)
【解析】
试题分析:(Ⅰ)由数列求得![]() 值,由周期求得
值,由周期求得![]() 值,由对称轴求得
值,由对称轴求得![]() 值,从而确定函数解析式;(Ⅱ)首先由正弦定理解三角形得到B的大小,代入函数式可求得函数值
值,从而确定函数解析式;(Ⅱ)首先由正弦定理解三角形得到B的大小,代入函数式可求得函数值![]()
试题解析:(Ⅰ)由已知,当n≥2时,an=1+3+5+…+(2n﹣1)=n2
而a1=1也符合an=n2,知a1=1,a2=4,所以函数y=f(x)的最小正周期为1,所以ω=2π,
则f(x)=4sin(2πx+φ),又函数y=f(x)的图象关于直线x=![]() 对称
对称
所以![]() φ=kπ+
φ=kπ+![]() (k∈z),因为|φ|<
(k∈z),因为|φ|<![]() ,所以φ=
,所以φ=![]() ,则f(x)=4sin(2πx+
,则f(x)=4sin(2πx+![]() )(6分)
)(6分)
(Ⅱ)由正弦定理计算B为![]() ,可得4sin(
,可得4sin(![]() +
+![]() )或4sin(
)或4sin(![]() +
+![]() ) (12分)
) (12分)


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程,在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为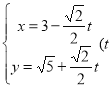 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极轴,以
为极轴,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的圆心到直线
的圆心到直线![]() 的距离;
的距离;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元。该公司第n年需要付出设备的维修和工人工资等费用![]() 的信息如下图。
的信息如下图。
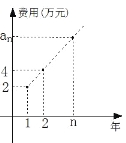
(Ⅰ)求![]() ;
;
(Ⅱ)引进这种设备后,第几年后该公司开始获利;
(Ⅲ)这种设备使用多少年,该公司的年平均获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等比数列![]() 的前n项和为Sn,已知a1=2,且4S1,3S2,2S3成等差数列.
的前n项和为Sn,已知a1=2,且4S1,3S2,2S3成等差数列.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有工人1000名,其中250名工人参加短期培训(称为![]() 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为![]() 类工人).现用分层抽样方法(按
类工人).现用分层抽样方法(按![]() 类,
类,![]() 类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(1)![]() 类工人和
类工人和![]() 类工人中个抽查多少工人?
类工人中个抽查多少工人?
(2)从![]() 类工人中的抽查结果和从
类工人中的抽查结果和从![]() 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.
表1:

表2:

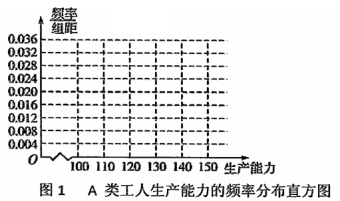
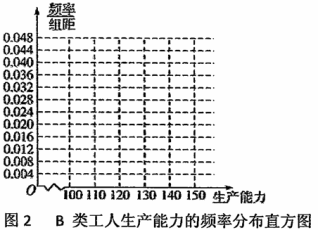
① 先确定![]() ,
,![]() ,再完成下列频率分布直方图,就生产能力而言,
,再完成下列频率分布直方图,就生产能力而言,![]() 类工人中个体间的差异程度与
类工人中个体间的差异程度与![]() 类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
② 分别估计![]() 类工人和
类工人和![]() 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中
的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的方程:
的方程:![]()
(1)求m的取值范围;
(2)若圆C与直线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,求
,求![]() 的值
的值
(3)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂经过市场调查,甲产品的日销售量![]() (单位:吨)与销售价格
(单位:吨)与销售价格![]() (单位:万元/吨)满足关系式
(单位:万元/吨)满足关系式 (其中
(其中![]() 为常数),已知销售价格为
为常数),已知销售价格为![]() 万元/吨时,每天可售出该产品
万元/吨时,每天可售出该产品![]() 吨.
吨.
(1)求![]() 的值;
的值;
(2)若该产品的成本价格为![]() 万元/吨,当销售价格为多少时,该产品每天的利润最大?并求出最大值.
万元/吨,当销售价格为多少时,该产品每天的利润最大?并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com