
【题目】已知对数函数![]() 过定点
过定点![]() (其中
(其中![]() ),函数
),函数![]() (其中
(其中![]() 为
为![]() 的导函数,
的导函数,![]() ,
,![]() 为常数)
为常数)
(1)讨论![]() 的单调性;
的单调性;
(2)若对![]() 有
有![]() 恒成立,且
恒成立,且![]() 在
在![]() (
(![]() )处的导数相等,求证:
)处的导数相等,求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】从抛物线![]() 上各点向x轴作垂线,垂线段中点的轨迹为E.
上各点向x轴作垂线,垂线段中点的轨迹为E.

(1)求曲线E的方程;
(2)若直线![]() 与曲线E相交于A,B两点,求证:
与曲线E相交于A,B两点,求证:![]() ;
;
(3)若点F为曲线E的焦点,过点![]() 的直线与曲线E交于M,N两点,直线
的直线与曲线E交于M,N两点,直线![]() ,
,![]() 分别与曲线E交于C,D两点,设直线
分别与曲线E交于C,D两点,设直线![]() ,
,![]() 斜率分别为
斜率分别为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 为抛物线
为抛物线![]() 上一点.
上一点.
(1)若![]() ,求
,求![]()
(2)已知点![]() ,过点
,过点![]() 作直线
作直线![]() 分别交曲线
分别交曲线![]() 于
于![]() ,证明:在点
,证明:在点![]() 运动过程中,直线
运动过程中,直线![]() 始终过定点,并求出该定点.
始终过定点,并求出该定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】诚信是立身之本,道德之基,我校学生会创设了“诚信水站”,既便于学生用水,又推进诚信教育,并用“![]() ”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,如表为该水站连续十二周(共三个周期)的诚信数据统计:
”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,如表为该水站连续十二周(共三个周期)的诚信数据统计:
第一周 | 第二周 | 第三周 | 第四周 | |
第一周期 |
|
|
|
|
第二周期 |
|
|
|
|
第三周期 |
|
|
|
|
(Ⅰ)计算表中十二周“水站诚信度”的平均数![]() ;
;
(Ⅱ)若定义水站诚信度高于![]() 的为“高诚信度”,
的为“高诚信度”,![]() 以下为“一般信度”则从每个周期的前两周中随机抽取两周进行调研,计算恰有两周是“高诚信度”的概率;
以下为“一般信度”则从每个周期的前两周中随机抽取两周进行调研,计算恰有两周是“高诚信度”的概率;
(Ⅲ)已知学生会分别在第一个周期的第四周末和第二个周期的第四周末各举行了一次“以诚信为本”的主题教育活动,根据已有数据,说明两次主题教育活动的宣传效果,并根据已有数据陈述理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】绝大部分人都有患呼吸系统疾病的经历,现在我们调查患呼吸系统疾病是否和所处环境有关.一共调查了![]() 人,患有呼吸系统疾病的
人,患有呼吸系统疾病的![]() 人,其中
人,其中![]() 人在室外工作,
人在室外工作,![]() 人在室内工作.没有患呼吸系统疾病的
人在室内工作.没有患呼吸系统疾病的![]() 人,其中
人,其中![]() 人在室外工作,
人在室外工作,![]() 人在室内工作.
人在室内工作.
(1)现采用分层抽样从室内工作的居民中抽取一个容量为![]() 的样本,将该样本看成一个总体,从中随机的抽取两人,求两人都有呼吸系统疾病的概率.
的样本,将该样本看成一个总体,从中随机的抽取两人,求两人都有呼吸系统疾病的概率.
(2)你能否在犯错误率不超过![]() 的前提下认为感染呼吸系统疾病与工作场所有关;
的前提下认为感染呼吸系统疾病与工作场所有关;
附表:
|
|
|
|
|
|
|
|
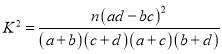
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆:![]() 的离心率为
的离心率为![]() ,y轴于椭圆相交于A、B两点,
,y轴于椭圆相交于A、B两点,![]() ,C、D是椭圆上异于A、B的任意两点,且直线AC、BD相交于点M,直线AD、BC相交于点N.
,C、D是椭圆上异于A、B的任意两点,且直线AC、BD相交于点M,直线AD、BC相交于点N.
![]() 求椭圆的方程;
求椭圆的方程;
![]() 求直线MN的斜率.
求直线MN的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,如图4①,②,③,④为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.

(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭记录了未使用节水龙头30天的日用水量数据(单位:![]() )和使用了节水龙头30天的日用水量数据,得到频数分布表如下:
)和使用了节水龙头30天的日用水量数据,得到频数分布表如下:
(一)未使用节水龙头30天的日用水量频数分布表
日用水量 |
|
|
|
|
|
频数 | 2 | 3 | 8 | 12 | 5 |
(二)使用了节水龙头30天的日用水量频数分布表
日用水量 |
|
|
|
|
|
频数 | 2 | 5 | 11 | 6 | 6 |
(1)估计该家庭使用了节水龙头后,日用水量小于![]() 的概率;
的概率;
(2)估计该家庭使用节水龙头后,平均每天能节省多少水?(同一组中的数据以这组数据所在区间中点的值作代表)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com