设函数f(x)=xn(n≥2,n∈N*)
(1)若Fn(x)=f(x-a)+f(b-x)(0<a<x<b),求Fn(x)的取值范围;
(2)若Fn(x)=f(x-b)-f(x-a),对任意n≥a (2≥a>b>0),证明:F(n)≥n(a-b)(n-b)n-2.
【答案】
分析:(1)利用已知条件,通过F
n(x)=f(x-a)+f(b-x)(0<a<x<b),化简函数的表达式,通过函数的单调性,求出函数F
n(x)的取值范围;
(2)利用F
n(x)=f(x-b)-f(x-a),x≥a>0,n≥a,说明函数的单调性,对任意n≥a (2≥a>b>0),利用作商法累加法,直接证明:F(n)≥n(a-b)(n-b)
n-2.
解答:解:(1)∵F
n(x)=f (x-a)+f(b-x)=(x-a)
n+(b-x)
nF
n(x)=n(x-a)
n-1+n(b-x)
n-1•(-1)=n[(x-a)
n-1-(b-x)
n-1]
令F
n(x)=0得(x-a)
n-1=(b-x)
n-1∵0<a<x<b∴f (x)=x
n(n≥2,n∈N
+)为单调增函数
∴x=
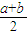
| x | (a,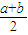 ) ) | 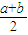 | (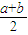 ,b) ,b) |
| Fn(x) | - | | + |
| Fn(x) | 单调减 | 极小值 | 单调增 |
∴F
n(x)
min=F
n(

)=(
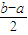
)
n+(
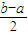
)
n=
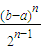
又F
n(x)在x=a,x=b处连续且F
n(a)=F
n(b)=(b-a)
n故
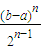
≤F
n(x)<(b-a)
n即F
n(x)的取值范围为[

,(b-a)
n)…(7分)
(2)证明:∵F
n(x)=f(x-b)-f(x-a)=(x-b)
n-(x-a)
n∴F
n(x)=n[(x-b)
n-1-(x-a)
n-1]
则F
n(n)=n[(n-b)
n-1-(n-a)
n-1]
∵当x≥a>0时F(x)>0
∴当x≥a>0时F
n(x)是关于x的增函数
∴当n≥a时,(n+1-b)
n-(n+1-a)
n>(n-b)
n-(n-a)
n>0
∴F
n(n+1)=(n+1)[(n+1-b)
n-(n+1-a)
n]>(n+1)[(n-b)
n-(n-a)
n]
>(n+1)[(n-b) (n-b)
n-1-(n-b) (n-a)
n-1]
=(n+1)(n-b)[(n-b)
n-1-(n-a)
n-1]
=
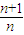
(n-b)•F(n)
而F
n(n)>0
于是
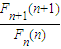
>

•(n-b)
而F(2)=2[(2-b)
2-1-(2-a)
2-1]=2(a-b)
当n≥3时
F(n)=

•

…

•F(2)
>
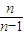
•
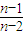
…

•2(a-b)•(n-b)
n-2=n(a-b)(n-b)
n-2即F(n)≥n(a-b)(n-b)
n-2…(14分)
点评:本题是中档题,考查函数的单调性,解析式的化简,函数的值域的求法,作商法累积法是证明本题的关键,考查发现问题解决问题的能力,注意转化思想的应用.

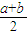
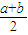 )
)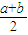
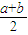 ,b)
,b) )=(
)=(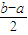 )n+(
)n+(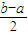 )n=
)n=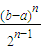
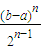 ≤Fn(x)<(b-a)n
≤Fn(x)<(b-a)n ,(b-a)n)…(7分)
,(b-a)n)…(7分)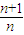 (n-b)•F(n)
(n-b)•F(n)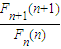 >
> •(n-b)
•(n-b) •
• …
… •F(2)
•F(2)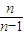 •
•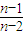 …
… •2(a-b)•(n-b)n-2
•2(a-b)•(n-b)n-2

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案 ,1)内( )
,1)内( ) ,1)内( )
,1)内( )