Question

【题目】甲、乙两位同学参加数学应用知识竞赛培训，现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次，记录如下：

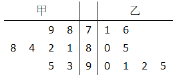
（Ⅰ）分别估计甲、乙两名同学在培训期间所有测试成绩的平均分；

（Ⅱ）从上图中甲、乙两名同学高于85分的成绩中各选一个成绩作为参考，求甲、乙两人成绩都在90分以上的概率；

（Ⅲ）现要从甲、乙中选派一人参加正式比赛，根据所抽取的两组数据分析，你认为选派哪位同学参加较为合适？说明理由.

Answer 1

【答案】（Ⅰ）（Ⅱ）（Ⅲ）见解析

【解析】

（Ⅰ）由茎叶图中的数据计算、，进而可得平均分的估计值；

（Ⅱ）求出基本事件数，计算所求的概率值；

（Ⅲ）答案不唯一.从平均数与方差考虑，派甲参赛比较合适；从成绩优秀情况分析，派乙参赛比较合适.

（Ⅰ）由茎叶图中的数据，计算，

，

由样本估计总体得，甲、乙两名同学在培训期间所有测试成绩的平均分分别均约为分.

（Ⅱ）从甲、乙两名同学高于分的成绩中各选一个成绩，基本事件是，

甲、乙两名同学成绩都在分以上的基本事件为，

故所求的概率为.

（Ⅲ）答案不唯一.

派甲参赛比较合适，理由如下：

由（Ⅰ）知，，

，

，

因为，，

所有甲的成绩较稳定，派甲参赛比较合适；

派乙参赛比较合适，理由如下：

从统计的角度看，甲获得分以上（含分）的频率为，

乙获得分以上（含分）的频率为，

因为，所有派乙参赛比较合适.