
【题目】已知![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)证明:![]() .
.
【答案】(1)见解析(2)见解析
【解析】
(1)由函数的解析式求得函数的定义域,再求出![]() ,分类讨论
,分类讨论![]() 的范围,求得
的范围,求得![]() 的符号,从而求得函数
的符号,从而求得函数![]() 的单调区间.
的单调区间.
(2)利用导数求得![]() 在区间
在区间![]() 单调递减,可得当
单调递减,可得当![]() 时,有
时,有![]() ,再用放缩法证得
,再用放缩法证得![]() ,从而证得要证的不等式成立.
,从而证得要证的不等式成立.
(1)![]() 的定义域为
的定义域为![]() ,
,
![]() .
.
令![]() ,可得
,可得![]() 或
或![]() .
.
当![]() 时,
时,![]() ,由
,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
由此可得![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
当![]() 时,
时,![]() ,由
,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
由此可得![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
当![]() 时,
时,![]() ,由
,由![]() 得
得![]() ,由
,由![]() 得
得![]() 或
或![]() ,由此可得
,由此可得![]() 的单调递增区间为
的单调递增区间为![]() ,
,
单调递减区间为![]() ,
,![]() .
.
当![]() 时,
时,![]() ,可得
,可得![]() ,故
,故![]() 的单调递减区间为
的单调递减区间为![]() .
.
当![]() 时,
时,![]() ,由
,由![]() 得
得![]() ,
,
由![]() 得
得![]() 或
或![]() ,由此可得
,由此可得![]() 的单调递增区间为
的单调递增区间为![]() ,
,
单调递减区间为![]() ,
,![]() ;
;
(2)当![]() 时,由(1)得
时,由(1)得![]() 在区间
在区间![]() 单调递减,
单调递减,
由此可得当![]() 时
时![]() ,即
,即![]() .
.
令![]() ,则
,则![]() ,
,
从而![]()
![]()
![]() ,
,
由此得![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为ρ= 4cosθ,直线l的参数方程为
的极坐标方程为ρ= 4cosθ,直线l的参数方程为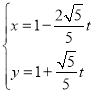 (t为参数).
(t为参数).
(1)求曲线![]() 的直角坐标方程及直线l的普通方程;
的直角坐标方程及直线l的普通方程;
(2)若曲线![]() 的参数方程为
的参数方程为![]() (α为参数),曲线
(α为参数),曲线![]() 上点P的极角为
上点P的极角为![]() Q为曲线
Q为曲线![]() 上的动点,求PQ的中点M到直线l距离的最大值.
上的动点,求PQ的中点M到直线l距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新能源汽车正以迅猛的势头发展,越来越多的企业不断推出纯电动产品,某汽车集团要对过去一年推出的四款纯电动车型中销量较低的![]() 车型进行产品更新换代.为了了解这种车型的外观设计是否需要改进,该集团委托某调查机构对大众做问卷调查,并从参与调查的人群中抽取了
车型进行产品更新换代.为了了解这种车型的外观设计是否需要改进,该集团委托某调查机构对大众做问卷调查,并从参与调查的人群中抽取了![]() 人进行抽样分析,得到如下表格:(单位:人)
人进行抽样分析,得到如下表格:(单位:人)
喜欢 | 不喜欢 | 合计 | |
青年人 |
|
|
|
中年人 |
|
|
|
合计 |
|
|
|
(1)根据表中数据,能否在犯错误的概率不超过![]() 的前提下认为大众对
的前提下认为大众对![]() 型车外观设计的喜欢与年龄有关?
型车外观设计的喜欢与年龄有关?
(2)现从所抽取的中年人中按是否喜欢![]() 型车外观设计利用分层抽样的方法抽取
型车外观设计利用分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机选出
人中随机选出![]() 人赠送五折优惠券,求选出的
人赠送五折优惠券,求选出的![]() 人中至少有
人中至少有![]() 人喜欢该集团
人喜欢该集团![]() 型车外观设计的概率;
型车外观设计的概率;
(3)将频率视为概率,从所有参与调查的人群中随机抽取![]() 人赠送礼品,记其中喜欢
人赠送礼品,记其中喜欢![]() 型车外观设计的人数为
型车外观设计的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式: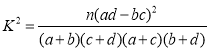 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:
满足:![]() ,且对任意的
,且对任意的![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )都有
)都有![]() ,则称数列
,则称数列![]() 为“G”数列.
为“G”数列.
(1)已知等比数列![]() 的通项为
的通项为![]() ,证明:
,证明:![]() 是“G”数列;
是“G”数列;
(2)记数列![]() 的前n项和为
的前n项和为![]() 且有
且有![]() ,若对每一个
,若对每一个![]() 取
取![]() ,
,![]() 中的较小者组成新的数列
中的较小者组成新的数列![]() ,若数列
,若数列![]() 为“G”数列,求实数
为“G”数列,求实数![]() 的取值范围?
的取值范围?
(3)若数列![]() 是“G”数列,且数列
是“G”数列,且数列![]() 的前n项之积
的前n项之积![]() 满足
满足![]() ,求证:数列
,求证:数列![]() 是等比数列.
是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .现以极点
.现以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为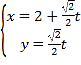 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标系方程和直线
的直角坐标系方程和直线![]() 的普通方程;
的普通方程;
(2)点![]() 在曲线
在曲线![]() 上,且到直线
上,且到直线![]() 的距离为
的距离为![]() ,求符合条件的
,求符合条件的![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 和
和![]() 两点.
两点.
(1)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)若过点![]() 且垂直于直线
且垂直于直线![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,记
两点,记![]() 与
与![]() 的面积分别为
的面积分别为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() ,已知椭圆离心率为
,已知椭圆离心率为![]() ,过点
,过点![]() 且与
且与![]() 轴垂直的直线被椭圆截得的线段长为3.
轴垂直的直线被椭圆截得的线段长为3.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线
,求直线![]() 斜率的取值范围.
斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某公司![]() 年
年![]() 月份研发费用
月份研发费用![]() (百万元)和产品销量
(百万元)和产品销量![]() (万台)的具体数据:
(万台)的具体数据:
月 份 |
|
|
|
|
|
|
|
|
研发费用(百万元) |
|
|
|
|
|
|
|
|
产品销量(万台) |
|
|
|
|
|
|
|
|
(1)根据数据可知![]() 与
与![]() 之间存在线性相关关系,用线性相关系数说明
之间存在线性相关关系,用线性相关系数说明![]() 与
与![]() 之间的相关性强弱程度
之间的相关性强弱程度
(2)求出![]() 与
与![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() ),并估计当研发费用为
),并估计当研发费用为![]() (百万元)时该产品的销量.
(百万元)时该产品的销量.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
参照公式:相关系数 ,其回归直线
,其回归直线![]() 中的
中的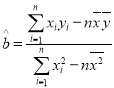
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com