练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知数列为等差数列，，.

    （1） 求数列的通项公式;

    （2）求数列的前n项和.

    【答案】（1）；（2）.

    【解析】试题分析：利用等差数列通项公式列出方程组，求出首项和公差，由此能求出数列的

    通项公式；（2）由（1）可得，利用错位相减法及等比数列前项和公式能求出数列的前n项和.

    试题解析： (1)设数列的公差为，依题意得方程组解得.

    所以的通项公式为.

    （2）由（1）可得，

    －得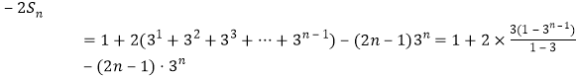

    所以.

    【 方法点睛】本题主要考查等差数列的通项公式、等比数列的求和公式以及错位相减法求数列的前 项和，属于中档题.一般地，如果数列是等差数列，是等比数列，求数列的前项和时，可采用“错位相减法”求和，一般是和式两边同乘以等比数列的公比，然后作差求解, 在写出“”与“” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“”的表达式.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= sinωx+cosωx（ω＞0）的图象与直线y=﹣2的两个相邻公共点之间的距离等于π，则f（x）的单调递减区间是（ ）
    A.[kπ+ ，kπ+ ]，k∈z
    B.[kπ﹣ ，kπ+ ]，k∈z
    C.[2kπ+ ，2kπ+ ]，k∈z
    D.[2kπ﹣ ，2kπ+ ]，k∈z

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数定义在上且满足下列两个条件:

    ①对任意都有;

    ②当时,有，

    （1）求，并证明函数在上是奇函数；

    （2）验证函数是否满足这些条件；

    （3）若，试求函数的零点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】 在平行四边形ABCD中，A(1，1)，＝(6，0)，点M是线段AB的中点，线段CM与BD交于点P．(1) 若＝(3，5)，求点C的坐标；(2) 当||＝||时，求点P的轨迹．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）设．

    ①若，求函数的零点；

    ②若函数存在零点，求的取值范围．

    （2）设，若对任意恒成立，试求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）已知：“直线与圆相交”； ：“有一正根和一负根”.若为真， 为真，求的取值范围.

    （2）已知椭圆： 与圆： ，双曲线与椭圆有相同的焦点，它的两条渐近线恰好与圆相切.求双曲线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形为正方形， 平面， ， .试结合向量法：（1）证明：平面平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两同学利用暑假到某县进行社会实践，对该县的养鸡场连续六年来的规模进行调查研究，得到如下两个不同的信息图：

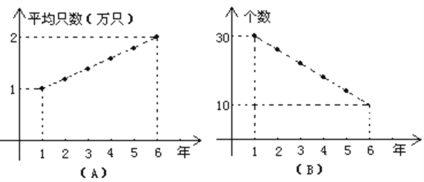
    （A）图表明：从第1年平均每个养鸡场出产1万只鸡上升到第6年平均每个养鸡场出产2万只鸡：

    （B）图表明：由第1年养鸡场个数30个减少到第6年的10个.

    请你根据提供的信息解答下列问题：

    （1）第二年的养鸡场的个数及全县出产鸡的总只数各是多少？

    （2）哪一年的规模最大？为什么？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=x3+bx2+cx+d图象如图，则函数 的单调递减区间为（ ）

    A.（﹣∞，﹣2）
    B.[3，+∞）
    C.[﹣2，3]
    D.[ ）

    查看答案和解析>>

    同步练习册答案