
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).在以坐标原点为极点,
).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() .
.
(1)说明![]() 是哪种曲线,并将
是哪种曲线,并将![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)已知![]() 与
与![]() 的交于
的交于![]() ,
,![]() 两点,且
两点,且![]() 过极点,求线段
过极点,求线段![]() 的长.
的长.
【答案】(Ⅰ)![]() 为以
为以![]() 为圆心,以
为圆心,以![]() 为半径的圆;
为半径的圆;![]()
(Ⅱ)![]()
【解析】
试题分析:
(1)为知![]() 是哪种曲线,需将
是哪种曲线,需将![]() 的参数方程化为普通方程,再将普通方程化为极坐标方程.(2)先将
的参数方程化为普通方程,再将普通方程化为极坐标方程.(2)先将![]() 与
与![]() 方程化为普通方程,易知AB为
方程化为普通方程,易知AB为![]() 与
与![]() 的公共弦长,在求出弦AB的方程后,由点到直线的距离公式求出C2(0,1)到公共弦的距离为
的公共弦长,在求出弦AB的方程后,由点到直线的距离公式求出C2(0,1)到公共弦的距离为![]() ,由勾股定理即可求出
,由勾股定理即可求出![]()
试题解析:
解:(1)∵曲线C1的参数方程为![]() (t为参数,a>0).
(t为参数,a>0).
∴C1的普通方程为![]() ,
,
∴C1为以C1(![]() ,0)为圆心,以a为半径的圆,
,0)为圆心,以a为半径的圆,
由ρ2=x2+y2,x=ρcosθ,y=ρsinθ,得C1的极坐标方程为![]() .
.
(2)解法一:∵曲线![]() .
.
∴![]() ,
,
二者相减得公共弦方程为![]() ,
,
∵AB过极点,∴公共弦方程![]() 过原点,
过原点,
∵a>0,∴a=3,∴公共弦方程为![]() ,
,
则C2(0,1)到公共弦的距离为![]() .
.
∴![]() .
.
解法二:∵AB:θ=θ0,
∴![]() 与ρ2=2ρsinθ+6为ρ的同解方程,
与ρ2=2ρsinθ+6为ρ的同解方程,
∴![]() 或θ=
或θ=![]() .
.
∴![]() .
.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】新高考3+3最大的特点就是取消文理科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全理(选择物理、化学、生物)的选择是否与性别有关决定从某学校高一年级的650名学生中随机抽取男生、女生各25人进行模拟选科经统计,选择全理的人数比不选全理的人数多10人
(1)请完成下面的2×2列联表;
选择全理 | 不选择全理 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
(2)估计有多大把握认为选择全理与性别有关,并说明理由.
附: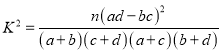 ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,侧面
,侧面![]() 为正三角形,侧面
为正三角形,侧面![]() 底面
底面![]() ,
,![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 的中点.
的中点.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲、乙等5人排成一排照相,按下列要求各有多少种不同的排法?求:
(1)甲、乙不能相邻;
(2)甲、乙相邻且都不站在两端;
(3)甲、乙之间仅相隔1人;
(4)按高个子站中间,两侧依次变矮(五人个子各不相同)的顺序排列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为庆祝国庆节,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名,将其成绩(成绩均为整数)分成[40,50),[50,60),…,[90,100)六组,并画出如图所示的部分频率分布直方图,观察图形,回答下列问题:

(1)求第四组的频率,并补全这个频率分布直方图;
(2)请根据频率分布直方图,估计样本的众数、中位数和平均数.(每组数据以区间的中点值为代表)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com