
(本小题共l4分)
已知函数 ,
,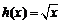 .
.
(Ⅰ)设函数F(x)=18f(x)-x2[h(x)]2,求F(x)的单调区间与极值;
(Ⅱ)设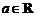 ,解关于x的方程
,解关于x的方程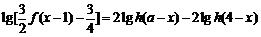 ;
;
(Ⅲ)设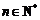 ,证明:
,证明: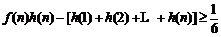 .
.
本小题主要考查函数导数的应用、不等式的证明、解方程等基础知识,考查数形结合、函数与方程、分类与整合等数学思想方法及推理运算、分析问题、解决问题的能力.
解:(Ⅰ)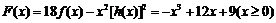 ,
,
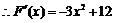 .
.
令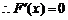 ,得
,得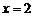 (
( 舍去).
舍去).
当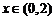 时.
时.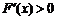 ;当
;当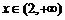 时,
时,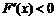 ,
,
故当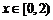 时,
时,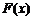 为增函数;当
为增函数;当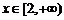 时,
时,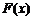 为减函数.
为减函数.
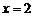 为
为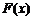 的极大值点,且
的极大值点,且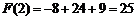 .
.
(Ⅱ)方法一:原方程可化为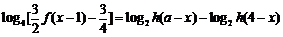 ,
,
即为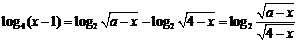 ,且
,且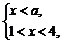
①当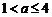 时,
时,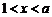 ,则
,则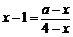 ,即
,即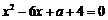 ,
,
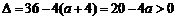 ,此时
,此时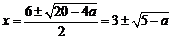 ,∵
,∵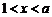 ,
,
此时方程仅有一解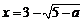 .
.
②当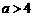 时,
时,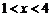 ,由
,由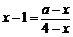 ,得
,得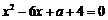 ,
, ,
,
若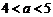 ,则
,则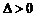 ,方程有两解
,方程有两解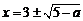 ;
;
若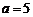 时,则
时,则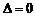 ,方程有一解
,方程有一解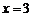 ;
;
若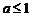 或
或 ,原方程无解.
,原方程无解.
方法二:原方程可化为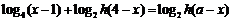 ,
,
即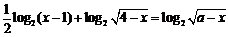 ,
,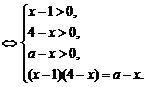
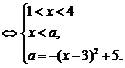
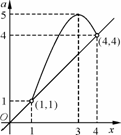 ①当
①当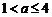 时,原方程有一解
时,原方程有一解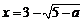 ;
;
②当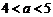 时,原方程有二解
时,原方程有二解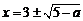 ;
;
③当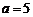 时,原方程有一解
时,原方程有一解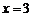 ;
;
④当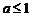 或
或 时,原方程无解.
时,原方程无解.
(Ⅲ)由已知得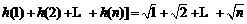 ,
,
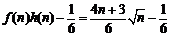 .
.
设数列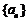 的前n项和为
的前n项和为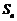 ,且
,且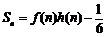 (
(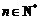 )
)
从而有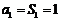 ,当
,当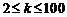 时,
时, .
.
又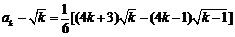
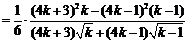
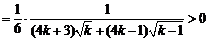 .
.
即对任意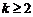 时,有
时,有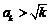 ,又因为
,又因为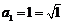 ,所以
,所以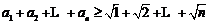 .
.
则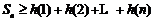 ,故原不等式成立.
,故原不等式成立.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源:2011年普通高中招生考试四川省市高考文科数学 题型:解答题
(本小题共l4分)
已知 函数
函数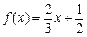 ,
,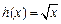 .
.
(Ⅰ)设函数F(x)=18f(x)-x2[h(x)]2,求F(x)的单调区间与极值;
(Ⅱ)设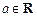 ,解关于x的方程
,解关于x的方程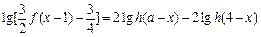 ;
;
(Ⅲ)设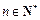 ,证明:
,证明: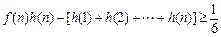 .
.
查看答案和解析>>
科目:高中数学 来源:2011年四川省普通高等学校招生统一考试理科数学 题型:解答题
(本小题共l4分)
已知 函数f(x)=
函数f(x)= 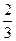 x
x  +
+ 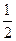 , h(x)=
, h(x)= 
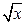 .
.
(I)设函数F(x)=f(x)一h(x),求F(x)的单调区间与极值;
(Ⅱ)设a∈R,解关于x的方程log4 [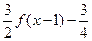 ]=1og2 h(a-x)一log2h (4-x);
]=1og2 h(a-x)一log2h (4-x);
(Ⅲ)试比较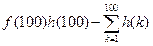 与
与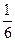 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2011年四川省招生统一考试理科数学 题型:解答题
(本小题共l4分)
已知函数f(x)=  x +
x +  , h(x)=
, h(x)=  .
.
(I)设函数F(x)=f(x)一h(x),求F(x)的单调区间与极值;
(Ⅱ)设a∈R,解关于x的方程log4 [ ]=1og2 h(a-x)一log2h (4-x);
]=1og2 h(a-x)一log2h (4-x);
(Ⅲ)试比较 与
与 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2011年高考试题数学理(四川卷)解析版 题型:解答题
(本小题共l4分)
已知函数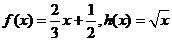
(I)设函数 ,求
,求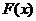 的单调区间与极值;
的单调区间与极值;
(Ⅱ)设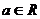 ,解关于
,解关于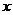 的方程
的方程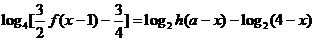
(Ⅲ)试比较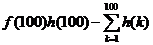 与
与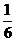 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com