
����Ŀ����֪����f��x��=lnx��x��0����
������֤��f��x����1�� ![]() ��
��
������g��x��=x2f��x�����ҹ���x�ķ���x2f��x��=m���������ȵ�ʵ��x1 �� x2��x1��x2����
��i����ʵ��m��ȡֵ��Χ��
��ii����֤��x1x22�� ![]() ��
��
���ο����ݣ�e=2.718�� ![]() ��0.960��
��0.960�� ![]() ��1.124��
��1.124�� ![]() ��0.769��ln2��0.693��ln2.6��0.956��ln2.639��0.970��ע����ͬ�ķ������ܻ�ѡȡ��ͬ�����ݣ�
��0.769��ln2��0.693��ln2.6��0.956��ln2.639��0.970��ע����ͬ�ķ������ܻ�ѡȡ��ͬ�����ݣ�
���𰸡��⣺��1��֤������h��x��=f��x����1+ ![]() =lnx��1+
=lnx��1+ ![]() ����x��0���� h�䣨x��=
����x��0���� h�䣨x��= ![]() =
= ![]() ��
��
x�ʣ�0��1��ʱ��h�䣨x����0��x�ʣ�1��+�ޣ���h�䣨x����0��
h��x���ڣ�0��1���ݼ����ڣ�1��+�ޣ�������
h��x����h��1��=0����f��x����1�� ![]() ������
������
����g��x��=x2f��x��=x2lnx����x��0��
��i��g�䣨x��=x��2lnx+1������g�䣨x��=0����x= ![]() ��
��
x ![]() ��ʱ��g�䣨x����0��x
��ʱ��g�䣨x����0��x ![]() ʱ��g�䣨x����0��
ʱ��g�䣨x����0��
��g��x���ڣ�0�� ![]() ���ݼ����ڣ�
���ݼ����ڣ� ![]() ������
������
g��x��min=g�� ![]() ��=��
��=�� ![]() ����x��0��ʱg��x����0��g��1��=0��
����x��0��ʱg��x����0��g��1��=0��
g��x����ͼ�����£�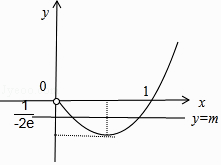
Ҫʹ����x�ķ���x2f��x��=m���������ȵ�ʵ��x1 �� x2��x1��x2����
ʵ��m��ȡֵ��ΧΪ������ ![]() ��0����
��0����
��ii��֤�����ɣ�i������f��x��=m��m����2������������ʵ��x1 �� x2 �� ���� 0��x1�� ![]() ��x2��1��
��x2��1��
��F��x��=x2lnx��m������F��x1���Tf��x2��
���캯��G��x��=F��x����F�� ![]() ��=x2lnx��
��=x2lnx�� ![]() ����
���� ![]() ��x��1����
��x��1����
G�䣨x����0����G�� ![]() ����0��
����0��
�� 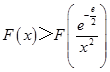 ��
�� ![]() ��x��1ʱ�������
��x��1ʱ�������
����F��x1��=F��x2�� 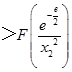 ����x1 ��
����x1 �� ![]() �ʣ�0��
�ʣ�0�� ![]() ��
��
�ɣ�i��֪F��x���ڣ�0�� ![]() ���ݼ�����
���ݼ����� 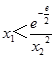 ��
��
��x1x22�� ![]()
��������������h��x��=f��x����1+ ![]() =lnx��1+
=lnx��1+ ![]() ����x��0����ȷ������h��x�������Լ���ֵ���ɣ�����g��x��=x2f��x��=x2lnx����x��0�� ��i��g�䣨x��=x��2lnx+1����ȷ��g��x���ĵ����ԣ�����g��x����ͼ�������ʵ��m��ȡֵ��Χ����ii���ɣ�i������f��x��=m��m����2������������ʵ��x1 �� x2 �� ���� 0��x1��
����x��0����ȷ������h��x�������Լ���ֵ���ɣ�����g��x��=x2f��x��=x2lnx����x��0�� ��i��g�䣨x��=x��2lnx+1����ȷ��g��x���ĵ����ԣ�����g��x����ͼ�������ʵ��m��ȡֵ��Χ����ii���ɣ�i������f��x��=m��m����2������������ʵ��x1 �� x2 �� ���� 0��x1�� ![]() ��x2��1����F��x��=x2lnx��m������F��x1���Tf��x2��
��x2��1����F��x��=x2lnx��m������F��x1���Tf��x2��
���캯��G��x��=F��x����F�� ![]() ��=x2lnx��
��=x2lnx�� ![]() ����
���� ![]() ��x��1����
��x��1����
���õ�����F��x1��=F��x2�� 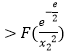 ����x1 ��
����x1 �� ![]() �ʣ�0��
�ʣ�0�� ![]() ��������֤��x1x22��
��������֤��x1x22�� ![]() ��
��
�����㾫����������Ĺؼ������������õ����о������ĵ����Ե����֪ʶ������һ���,�����ĵ��������䵼�������������¹�ϵ�� ��ij������![]() �ڣ�(1)���
�ڣ�(1)���![]() ����ô����
����ô����![]() ��������䵥��������(2)���
��������䵥��������(2)���![]() ����ô����
����ô����![]() ��������䵥���ݼ����Լ��Ժ����ļ�ֵ�뵼�������⣬�˽�����
��������䵥���ݼ����Լ��Ժ����ļ�ֵ�뵼�������⣬�˽�����![]() �ļ�ֵ�ķ�����:��1�������
�ļ�ֵ�ķ�����:��1�������![]() ���������
���������![]() ,�Ҳ�
,�Ҳ�![]() ,��ô
,��ô![]() �Ǽ���ֵ��2�������
�Ǽ���ֵ��2�������![]() ���������
���������![]() ,�Ҳ�
,�Ҳ�![]() ,��ô
,��ô![]() �Ǽ�Сֵ��
�Ǽ�Сֵ��


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB��DC��AD=AB=BC=1�� ![]() ��ƽ��ACFE��ƽ��ABCD���ı���ACFE�Ǿ��Σ�AE=1����M���߶�EF�ϣ�
��ƽ��ACFE��ƽ��ABCD���ı���ACFE�Ǿ��Σ�AE=1����M���߶�EF�ϣ� 
��1���� ![]() Ϊ��ֵʱ��AM��ƽ��BDF��֤����Ľ��ۣ�
Ϊ��ֵʱ��AM��ƽ��BDF��֤����Ľ��ۣ�
��2��������B��EF��D��ƽ��ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������f��x��=sin��2x�� ![]() ����ͼ������ƽ��
����ͼ������ƽ�� ![]() ����λ�õ�y=g��x����ͼ��������˵��������ǣ� ��
����λ�õ�y=g��x����ͼ��������˵��������ǣ� ��
A.y=g��x������С������Ϊ��
B.y=g��x����ͼ�����ֱ��x= ![]() �Գ�
�Գ�
C.y=g��x����[�� ![]() ��
�� ![]() ]�ϵ�������
]�ϵ�������
D.y=g��x����ͼ����ڵ㣨 ![]() ��0���Գ�
��0���Գ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��g��x��=b��x+1��������a��0��b��0
��g��x��=b��x+1��������a��0��b��0
��1����a=b������F��x��=f��x����g��x���ĵ������䣻
��2����֪����f��x���������뺯��g��x�����������������㣬����������ĺ�����ֱ�Ϊx1 �� x2 �� ֤���� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���Ӳ�Ʒ��˾ǰ�������������x����λ��ǧ��Ԫ������������y����λ���������������±���ʾ��
x����λ��ǧ��Ԫ�� | 1 | 2 | 3 | 4 |
y��������� | 3 | 5 | 6 | 9 |
������y����x�����Իع鷽��Ϊ ![]() =1.9x+1��
=1.9x+1��
�ο���ʽ���ع鷽�� ![]() =
= ![]() x+
x+ ![]() ��б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��![]() =
=  ��
�� ![]() =
= ![]() ��
�� ![]() ��
��
��1���ù�˾��һ����Ͷ��10ǧ��Ԫ�������ѣ���������õĻع鷽��Ԥ����һ���������m��
��2�������±���ʾ���ɢ�����ݣ����y����x�����Իع鷽�� ![]() =
= ![]() x+
x+ ![]() ��
��
x����λ��ǧ��Ԫ�� | 1 | 2 | 3 | 4 | 10 |
y��������� | 3 | 5 | 6 | 9 | m |
������С���˷���ԭ��˵�� ![]() =
= ![]() x+
x+ ![]() ��
�� ![]() =1.9x+1�Ĺ�ϵ��
=1.9x+1�Ĺ�ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ӹ���һ�Σ����¼�A=����������������ͬ����B=�����ٳ���һ��6�㡱�������P��A|B�����ڣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=e2x��x2��a��
��1��֤��f��x���ڣ����ޣ�+�ޣ���Ϊ��������
��2����a=1ʱ���ⲻ��ʽf[f��x��]��x��
��3����f[f��x����x2��2x]��f��x���ڣ�0��+�ޣ��Ϻ��������a���������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ABCD�У�AB��CD��AB��AD��AB=2CD=2AD=2���ڵ���ֱ��������CDE�У���C=90�㣬��M��N�ֱ�Ϊ�߶�BC��CE�ϵĶ��㣬�� ![]() �� ��
�� �� ![]() ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��= ![]() ��g��x��=a2lnx+b�й����㣬���ڹ����㴦�����߷�����ͬ����ʵ��b�����ֵΪ�� ��
��g��x��=a2lnx+b�й����㣬���ڹ����㴦�����߷�����ͬ����ʵ��b�����ֵΪ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com