
18.(乙)如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,
且∠C1CB=∠C1CD=∠BCD=![]() .
.
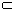
(Ⅰ)证明:C1C⊥BD;
(Ⅱ)假定CD=2,CC1=![]() ,记面C1BD为
,记面C1BD为![]() ,面CBD为
,面CBD为![]() ,求二面角
,求二面角![]() -BD-
-BD-![]() 的平面角的余弦值;
的平面角的余弦值;
(Ⅲ)当![]() 的值为多少时,能使A1C⊥平面C1BD?请给出证明.
的值为多少时,能使A1C⊥平面C1BD?请给出证明.
18.(乙)本小题主要考查直线与直线、直线与平面的关系,逻辑推理能力.
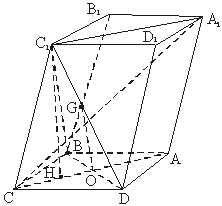
(Ⅰ)证明:连结A1C1、AC,AC和BD交于O,连结C1O.
∵四边形ABCD是菱形,
∴AC⊥BD,BC=CD.
又∵∠BCC1=∠DCC1,C1C=C1C,
∴△C1BC≌△C1DC,
∴C1B=C1D,
∵DO=OB,
∴C1O⊥BD,
但,AC⊥BD,AC∩C1O=O,
∴BD⊥平面AC1.
又C1C![]() 平面AC1,
平面AC1,
∴C1C⊥BD.
(Ⅱ)解:由(Ⅰ)知AC⊥BD,C1O⊥BD,
∴∠C1OC是二面角α—BD—β的平面角.
在△C1BC中,BC=2,C1C=![]() ,∠BCC1=60°,
,∠BCC1=60°,
∴C1B2=22+![]() -2×2×
-2×2×![]() ×cos60°=
×cos60°=![]() .
.
∵∠OCB=30°,
∴OB=![]() BC=1.
BC=1.
∴C1O2=C1B2-OB2=![]() -1=
-1=![]() ,
,
∴C1O=![]() 即C1O=C1C.
即C1O=C1C.
作C1H⊥OC,垂足为H.
∴点H是OC的中点,且OH=![]() ,
,
所以 cos∠C1OC=![]() =
=![]() .
.
(Ⅲ)当![]() =1时,能使A1C⊥平面C1BD.
=1时,能使A1C⊥平面C1BD.
证明一:∵![]() =1
=1
∴BC=CD=C1C,
又∠BCD=∠C1CB=∠C1CD,
由此可推得BD=C1B=C1D.
∴三棱锥C—C1BD是正三棱锥.
设A1C与C1O相交于G.
∵A1C1∥AC,且A1C1︰OC=2︰1,
∴C1G︰GO=2︰1.
又C1O是正三角形C1BD的BD边上的高和中线,
∴点G是正三角形C1BD的中心,
∴CG⊥平面C1BD.
即 A1C⊥平面C1BD.
证明二:由(Ⅰ)知,BD⊥平面AC1,
∵A1C![]() 平面AC1,∴BD⊥A1C.
平面AC1,∴BD⊥A1C.
当![]() =1时,平行六面体的六个面是全等的菱形,
=1时,平行六面体的六个面是全等的菱形,
同BD⊥A1C的证法可得BC1⊥A1C.
又 BD∩BC1=B,
∴A1C⊥平面C1BD.
【参考解法】(Ⅲ)
答:当![]() =1时,能使A1C⊥平面C1BD.
=1时,能使A1C⊥平面C1BD.
证明:∵![]() ∴BC=CD=C1C
∴BC=CD=C1C
又∠BCD=∠C1CB=∠C1CD
∴△CDC1≌△CBC1≌△CDB
∴BC1=C1D=BD
在平行六面体ABCD-A1B1C1D1中,
BC=CD=CC1,∠BCD=∠C1CB=∠C1CD=![]()
且ABCD是菱形,
∴它的六个面均是全等的菱形
∴A1C1=A1D=A1B
∴三棱锥A1-C1BD是正三棱锥
∴它的高A1G的垂足G是正三角形BDC1的中心,即A1G⊥底面BDC1于G
又三棱锥C-C1BD是正三棱锥
∴它的高CG的垂足也是正三角形BDC1的中心,即CG⊥底面BDC1于G,
∵A1G⊥底面BDC1于G,CG⊥底面BDC1于G,
∴直线A1G和直线CG重合,即A1、G、C共线,
∴A1C⊥平面C1BD.


科目:高中数学 来源:湖北省荆州中学2008高考复习立体几何基础题题库二(有详细答案)人教版 人教版 题型:044
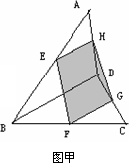
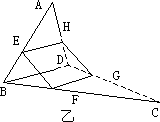
已知空间四边形ABCD中,E、H分别是AB、AD的中点.
(1)如图(甲)中,F、G分别是BC、CD的中点,求证:四边形EFGH是平行四边形;
(2)如图(乙)中,若F是BC上的点,G是DC上的点,且![]() ,求证:四边形EFGH是梯形,并且直线EF、GH、AC共点.
,求证:四边形EFGH是梯形,并且直线EF、GH、AC共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
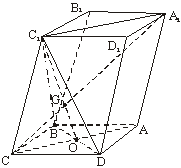
(Ⅰ)证明:C1C⊥BD;
(Ⅱ)当![]() 的值为多少时,能使A1C⊥平面C1BD?请给出证明.
的值为多少时,能使A1C⊥平面C1BD?请给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com