
【题目】在某单位的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格全部卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了80个面包,以x(单位:个,![]() )表示面包的需求量,T(单位:元)表示利润.
)表示面包的需求量,T(单位:元)表示利润.

(1)求食堂面包需求量的平均数;
(2)求T关于x的函数解析式;
(3)根据直方图估计利润T不少于100元的概率.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图的折线图为某小区小型超市今年一月份到五月份的营业额和支出数据(利润=营业额-支出),根据折线图,下列说法中正确的是( )

A.该超市这五个月中,利润随营业额的增长在增长
B.该超市这五个月中,利润基本保持不变
C.该超市这五个月中,三月份的利润最高
D.该超市这五个月中的营业额和支出呈正相关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一网站营销部为统计某市网友2017年12月12日在某网店的网购情况,随机抽查了该市60名网友在该网店的网购金额情况,如下表:
网购金额(单位:千元) | 频数 | 频率 | 网购金额(单位:千元) | 频数 | 频率 | |
[0,0.5) | 3 | 0.05 | [1.5,2) | 15 | 0.25 | |
[0.5,1) |
|
| [2,2.5) | 18 | 0.30 | |
[1,1.5) | 9 | 0.15 | [2.5,3] |
|
|
若将当日网购金额不小于2千元的网友称为“网购达人”,网购金额小于2千元的网友称为“网购探者”,已知“网购达人”与“网购探者”人数的比例为2:3.
(1)确定![]() ,
,![]() ,
,![]() ,
,![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;

(2)①.试根据频率分布直方图估算这60名网友当日在该网店网购金额的平均数和中位数;
②.若平均数和中位数至少有一个不低于2千元,则该网店当日评为“皇冠店”,试判断该网店当日能否被评为“皇冠店”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 图象的相邻两条对称轴之间的距离为
图象的相邻两条对称轴之间的距离为![]() .
.
(1)讨论函数f(x)在区间![]() 上的单调性;
上的单调性;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的![]() 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数![]() 的图象.求
的图象.求![]() 在
在![]() 上的值域.
上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名篮球运动员,甲投篮一次命中的概率为![]() ,乙投篮一次命中的概率为
,乙投篮一次命中的概率为![]() ,若甲、乙各投篮三次,设
,若甲、乙各投篮三次,设![]() 为甲、乙投篮命中的次数的差的绝对值,其中甲、乙两人投篮是否命中相互没有影响.
为甲、乙投篮命中的次数的差的绝对值,其中甲、乙两人投篮是否命中相互没有影响.
(1)若甲、乙第一次投篮都命中,求甲获胜(甲投篮命中数比乙多)的概率;
(2)求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() (
(![]() 为坐标原点),直线
为坐标原点),直线![]() .
.
(1)过直线![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
(2)过点![]() 的直线
的直线![]() 分别与圆
分别与圆![]() 交于点
交于点![]() (
(![]() 不与
不与![]() 重合),若
重合),若![]() ,试问直线
,试问直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() (如图),则( )
(如图),则( )
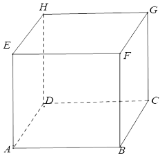
A.直线CF与GD所成的角与向量所成的角![]() 相等
相等
B.向量![]() 是平面ACH的法向量
是平面ACH的法向量
C.直线CE与平面ACH所成角的正弦值与![]() 的平方和等于1
的平方和等于1
D.二面角![]() 的余弦值等于
的余弦值等于![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() 是椭圆上一动点(与左、右顶点不重合).已知
是椭圆上一动点(与左、右顶点不重合).已知![]() 的面积的最大值为
的面积的最大值为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,过
两点,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 与另一点
与另一点![]() (
(![]() 不与
不与![]() 、
、![]() 重合).设
重合).设![]() 的外心为
的外心为![]() ,求证
,求证![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com