Question

【题目】已知中心在原点,焦点在x轴上的椭圆C的离心率为,点(0,)是椭圆与y轴的一个交点.

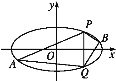
(1)求椭圆C的方程;

(2)直线x=2与椭圆交于P,Q两点,点P位于第一象限,A,B是椭圆上位于直线x=2两侧的动点;

①若直线AB的斜率为,求四边形APBQ面积的取值范围;

②当点A,B在椭圆上运动,且满足∠APQ=∠BPQ时,直线AB的斜率是否为定值?若是,求出此定值;若不是,说明理由.

Answer 1

【答案】（1）；（2）见解析

【解析】

⑴设椭圆的方程为=1(a>b>0)，由椭圆的性质求出，由此求得椭圆的方程

⑵①设A(x1,y1),B(x2,y2)，直线AB的方程为，与椭圆联立，得到，由此利用韦达定理，弦长公式求出四边形APBQ的面积的取值范围

②当时，设直线PA的方程为，分别与椭圆方程联立，利用韦达定理即可求得答案

(1)设椭圆的方程为=1(a>b>0),由题意可知,b=,a2=b2+c2,解得a=2,

∴椭圆C的方程为=1.

(2)①设A(x1,y1),B(x2,y2),直线AB的方程为y=x+t,

联立

消y可得,2x2+4tx+4t2-8=0,

即x2+2tx+2t2-4=0,

则有x1+x2=-2t,x1x2=2t2-4.

对于=1,令x=2,得P(2,1),Q(2,-1),

将P,Q分别代入直线可得,t=0,t=-2,

由点A,B在直线x=2的两侧,故-2<t<0,

四边形APBQ的面积为

S=S△APQ+S△BPQ

=|PQ|·|x2-x1|

=×2×|x2-x1|

=

=,

而-2<t<0,所以0<S四边形APBQ<4.

②当∠APQ=∠BPQ时,直线PA,PB的斜率之和为0,

不妨设直线PA的斜率为k,则直线PB的斜率为-k,

所以直线PA的方程为y-1=k(x-2),

即kx-y+1-2k=0,

联立

消去y可得,(1+4k2)x2+8k(1-2k)x+4(1-2k)2-8=0,

所以x1+2=.

同理直线PB的方程为y-1=-k(x-2),

可得,x2+2=,

所以x1+x2=,x1-x2=,

所以kAB=

=

=

=,

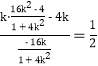故直线AB的斜率为定值.