
【题目】在长方体![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,E、F分别是线段AB、BC上的点,且
,E、F分别是线段AB、BC上的点,且![]() .
.
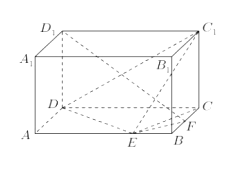
(1)求二面角![]() 的正切值;
的正切值;
(2)求直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
![]() 以A为原点,
以A为原点,![]() 分别为x轴,y轴,z轴的正向建立空间直角坐标系
分别为x轴,y轴,z轴的正向建立空间直角坐标系![]() ,写出要用的点的坐标,设出平面的法向量的坐标,根据法向量与平面上的向量垂直,利用数量积表示出两个向量的坐标之间的关系,求出平面的一个法向量,根据两个向量之间的夹角求出结果
,写出要用的点的坐标,设出平面的法向量的坐标,根据法向量与平面上的向量垂直,利用数量积表示出两个向量的坐标之间的关系,求出平面的一个法向量,根据两个向量之间的夹角求出结果![]() 把两条直线对应的点的坐标写出来,根据两个向量之间的夹角表示出异面直线的夹角.
把两条直线对应的点的坐标写出来,根据两个向量之间的夹角表示出异面直线的夹角.
![]() 以A为原点,
以A为原点,![]() 分别为x轴,y轴,z轴的正向建立空间直角坐标系,
分别为x轴,y轴,z轴的正向建立空间直角坐标系,
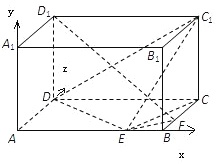
则有![]() 3,
3,![]() 、
、![]() 3,
3,![]() 、
、![]() 0,
0,![]() 、
、![]() 1,
1,![]() 、
、![]() 3,
3,![]()
于是,![]() 2,
2,![]()
设向量![]() 与平面
与平面![]() 垂直,
垂直,
则有
![]() ,其中
,其中![]()
取![]() 则
则![]() 是一个与平面
是一个与平面![]() 垂直的向量,
垂直的向量,
![]() 向量
向量![]() 0,
0,![]() 与平面CDE垂直,
与平面CDE垂直,
![]() 与
与![]() 所成的角
所成的角![]() 为二面角
为二面角![]() 的平面角
的平面角
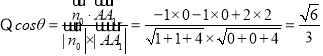
![]() ,
,
![]() 二面角
二面角![]() 的正切值为
的正切值为![]() ;
;
![]() 设
设![]() 与
与![]() 所成角为
所成角为![]() ,则
,则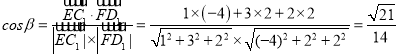 ,
,
![]() 直线
直线![]() 与
与![]() 所成的余弦值为
所成的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,一块长方形区域![]() ,
,![]() ,
,![]() ,在边
,在边![]() 的中点
的中点![]() 处有一个可转动的探照灯,其照射角
处有一个可转动的探照灯,其照射角![]() 始终为
始终为![]() ,设
,设![]() ,探照灯照射在长方形
,探照灯照射在长方形![]() 内部区域的面积为
内部区域的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,求
时,求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
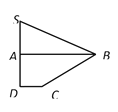
【题目】已知四边形![]() ,点
,点![]() 为线段
为线段![]() 的中点,且
的中点,且![]()
![]() .
. ![]() ,
, ![]() .现将△
.现将△![]() 沿
沿![]() 进行翻折,使得
进行翻折,使得![]()
![]() °,得到图形如图所示,连接
°,得到图形如图所示,连接![]() .
.
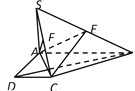
(Ⅰ)若点![]() 在线段
在线段![]() 上,证明:
上,证明: ![]() ;
;
(Ⅱ)若![]() 点为
点为![]() 的中点,求点
的中点,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在底面是正三角形、侧棱垂直于底面的三棱柱ABC﹣A1B1C1中,底面边长为a,侧棱长为2a,点M是A1B1的中点.
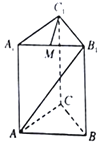
(1)证明:MC1⊥AB1.
(2)求直线AC1与侧面BB1C1C所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走人大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷![]() 广元某景点设有共享电动车租车点,共享电动车的收费标准是每小时2元
广元某景点设有共享电动车租车点,共享电动车的收费标准是每小时2元![]() 不足1小时的部分按1小时计算
不足1小时的部分按1小时计算![]() 甲、乙两人各租一辆电动车,若甲、乙不超过一小时还车的概率分别为
甲、乙两人各租一辆电动车,若甲、乙不超过一小时还车的概率分别为![]() ;一小时以上且不超过两小时还车的概率分别为
;一小时以上且不超过两小时还车的概率分别为![]() ;两人租车时间都不会超过三小时.
;两人租车时间都不会超过三小时.
![]() Ⅰ
Ⅰ![]() 求甲、乙两人所付租车费用相同的概率;
求甲、乙两人所付租车费用相同的概率;
![]() Ⅱ
Ⅱ![]() 设甲、乙两人所付的租车费用之和为随机变量
设甲、乙两人所付的租车费用之和为随机变量![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足条件
满足条件![]() ,且
,且![]()
(1)计算![]() ,请猜测数列
,请猜测数列![]() 的通项公式,并用数学归纳法证明;
的通项公式,并用数学归纳法证明;
(2)请分别构造一个二阶和三阶行列式,使它们的值均为![]() ,其中,要求所构造的三阶行列式主对角线下方的元素均为零,并用按某行或者某列展开的方法验证三阶行列式的值为
,其中,要求所构造的三阶行列式主对角线下方的元素均为零,并用按某行或者某列展开的方法验证三阶行列式的值为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com