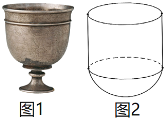
【题目】唐朝的狩猎景象浮雕银杯如图1所示.其浮雕临摹了国画、漆绘和墓室壁画，体现了古人的智慧与工艺.它的盛酒部分可以近似地看作是半球与圆柱的组合体（假设内壁表面光滑，忽略杯壁厚度），如图2所示.已知球的半径为R，酒杯内壁表面积为
,设酒杯上部分（圆柱）的体积为
，下部分（半球）的体积为
，则
（ ）
A.2B.
C.1D.
科目：高中数学 来源： 题型：
【题目】某公司采购了一批零件，为了检测这批零件是否合格，从中随机抽测120个零件的长度（单位：分米），按数据分成
，
，
，
，
，
这6组，得到如图所示的频率分布直方图，其中长度大于或等于1.59分米的零件有20个，其长度分别为1.59，1.59，1.61，1.61，1.62，1.63，1.63，1.64，1.65，1.65，1.65，1.65，1.66，1.67，1.68，1.69，1.69，1.71，1.72，1.74，以这120个零件在各组的长度的频率估计整批零件在各组长度的概率.
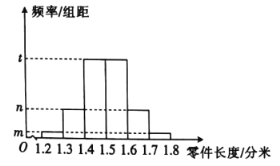
（1）求这批零件的长度大于1.60分米的频率，并求频率分布直方图中
，
，
的值；
（2）若从这批零件中随机选取3个，记
为抽取的零件长度在
的个数，求的分布列和数学期望；
（3）若变量
满足
且
，则称变量满足近似于正态分布
的概率分布.如果这批零件的长度
（单位：分米）满足近似于正态分布
的概率分布，则认为这批零件是合格的将顺利被签收；否则，公司将拒绝签收.试问，该批零件能否被签收？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
已知曲线
的参数方程为
（
为参数）.以直角坐标系的原点
为极点，
轴的正半轴为极轴建立坐标系，曲线
的极坐标方程为
.
（1）求的普通方程和的直角坐标方程；
（2）若过点
的直线
与交于
，
两点，与交于
，
两点，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某人坚持跑步锻炼，根据他最近20周的跑步数据，制成如下条形图：
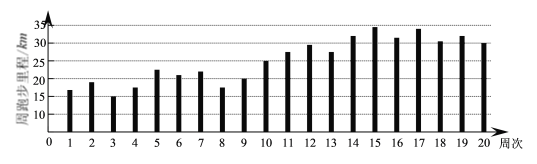
根据条形图判断，下列结论正确的是（ ）
A.周跑步里程逐渐增加
B.这20周跑步里程平均数大于30km
C.这20周跑步里程中位数大于30km
D.前10周的周跑步里程的极差大于后10周的周跑步里程的极差
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，四边形
为梯形， 
，且
， 
是边长为2的正三角形，顶点
在
上的射影为点
，且
， 
， 
.
（1）证明：平面
平面
；
（2）求二面角
的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线
的极坐标方程是
，以极点为原点，极轴为
轴的正半轴，建立平面直角坐标系，直线
过点
，倾斜角为
．
（1）求曲线的直角坐标方程与直线l的参数方程；
（2）设直线与曲线交于
，
两点，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
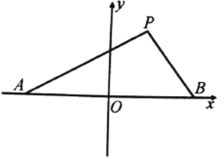
【题目】如图，设点
的坐标分别为
，直线
相交于点
，且它们的斜率之积为
．
（1）求点
的轨迹方程；
（2）设点
的轨迹为
，点
是轨迹为
上不同于
的两点，且满足
，求证：
的面积为定值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】法国数学家庞加是个喜欢吃面包的人，他每天都会购买一个面包，面包师声称自己出售的每个面包的平均质量是1000
，上下浮动不超过50.这句话用数学语言来表达就是：每个面包的质量服从期望为1000，标准差为50的正态分布.
（1）假设面包师的说法是真实的，从面包师出售的面包中任取两个，记取出的两个面包中质量大于1000的个数为
，求的分布列和数学期望；
（2）作为一个善于思考的数学家，庞加莱每天都会将买来的面包称重并记录，25天后，得到数据如下表，经计算25个面包总质量为24468.庞加莱购买的25个面包质量的统计数据（单位：）
981 | 972 | 966 | 992 | 1010 | 1008 | 954 | 952 | 969 | 978 |
989 | 1001 | 1006 | 957 | 952 | 969 | 981 | 984 | 952 | 959 |
987 | 1006 | 1000 | 977 | 966 |
尽管上述数据都落在
上，但庞加菜还是认为面包师撒谎，根据所附信息，从概率角度说明理由
附：
①若
，从X的取值中随机抽取25个数据，记这25个数据的平均值为Y，则由统计学知识可知：随机变量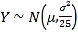
②若
，则
，
，
；
③通常把发生概率在0.05以下的事件称为小概率事件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
