
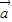 ,
,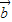 ,
,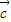 是任意的非零向量,且相互不共线,下列命题:
是任意的非零向量,且相互不共线,下列命题: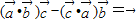 ,
,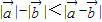 ,
,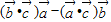 不与
不与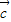 垂直,
垂直,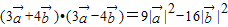 .
. ,
,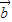 ,
,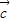 是任意的非零向量,且相互不共线,(1)中研究向量的数量积与数乘运算,由运算规则判断;
是任意的非零向量,且相互不共线,(1)中研究向量的数量积与数乘运算,由运算规则判断;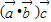 与
与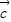 共线,
共线,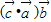 与
与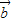 共线,由题设条件
共线,由题设条件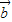 ,
,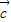 是任意的非零向量,且相互不共线知,
是任意的非零向量,且相互不共线知,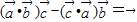 不成立;
不成立;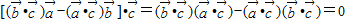 ,故
,故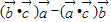 与
与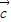 垂直,所以此命题不正确;
垂直,所以此命题不正确;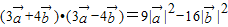 是正确的;
是正确的;

科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| b |
| c |
| c |
| a |
| b |
| 0 |
| a |
| b |
| a |
| b |
| b |
| c |
| a |
| a |
| c |
| b |
| c |
| a |
| b |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山西省大同一中高一(下)期中数学试卷(解析版) 题型:填空题
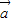 、
、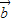 、
、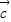 是任意的非零向量,且相互不共线,给定下列结论
是任意的非零向量,且相互不共线,给定下列结论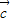 -•
-•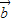 =
=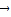
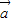 |-|
|-|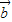 |<|
|<|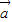 -
-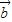 |
|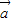 -•
-•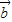 不与
不与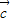 垂直
垂直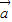 +2
+2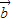 )•(3
)•(3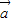 -2
-2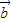 )=9
)=9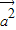 -4
-4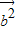
查看答案和解析>>
科目:高中数学 来源: 题型:
设![]() 、
、![]() 、
、![]() 是任意的非零向量,且互不共线,给出以下四个命题:
是任意的非零向量,且互不共线,给出以下四个命题:
①![]() ②
②![]() <
<![]() ③(
③(![]() ?
?![]() )?
)?![]() -(
-(![]() ?
?![]() )?
)?![]() 不与
不与![]() 垂直
垂直
④(3![]() +2
+2![]() )?(3
)?(3![]() -2
-2![]() )=9
)=9![]() -4
-4![]() 其中真命题的个数是
其中真命题的个数是
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com