
【题目】南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列.对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,5,11,21,37,6l,95,则该数列的第8项为( )
A.99B.131C.139D.141
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】《高中数学课程标准》(2017版)规定了数学直观想象学科的六大核心素养,为了比较甲、乙两名高二学生的数学核心素养水平,现以六大素养为指标对二人进行了测验,根据测验结果绘制了雷达图(如图,每项指标值满分为5分,分值高者为优),则下面叙述正确的是(注:雷达图![]() ,又可称为戴布拉图、蜘蛛网图
,又可称为戴布拉图、蜘蛛网图![]() ,可用于对研究对象的多维分析)( )
,可用于对研究对象的多维分析)( )
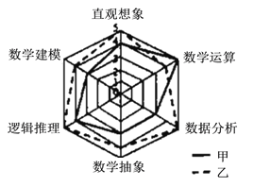
A.甲的直观想象素养高于乙
B.甲的数学建模素养优于数据分析素养
C.乙的数学建模素养与数学运算素养一样
D.乙的六大素养整体水平低于甲
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设无穷数列![]() 的每一项均为正数,对于给定的正整数
的每一项均为正数,对于给定的正整数![]() ,
,![]() (
(![]() ),若
),若![]() 是等比数列,则称
是等比数列,则称![]() 为
为![]() 数列.
数列.
(1)求证:若![]() 是无穷等比数列,则
是无穷等比数列,则![]() 是
是![]() 数列;
数列;
(2)请你写出一个不是等比数列的![]() 数列的通项公式;
数列的通项公式;
(3)设![]() 为
为![]() 数列,且满足
数列,且满足![]() ,请用数学归纳法证明:
,请用数学归纳法证明:![]() 是等比数列.
是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】成都七中为了解班级卫生教育系列活动的成效,对全校40个班级进行了一次突击班级卫生量化打分检查(满分100分,最低分20分).根据检查结果:得分在![]() 评定为“优”,奖励3面小红旗;得分在
评定为“优”,奖励3面小红旗;得分在![]() 评定为“良”,奖励2面小红旗;得分在
评定为“良”,奖励2面小红旗;得分在![]() 评定为“中”,奖励1面小红旗;得分在
评定为“中”,奖励1面小红旗;得分在![]() 评定为“差”,不奖励小红旗.已知统计结果的部分频率分布直方图如图:
评定为“差”,不奖励小红旗.已知统计结果的部分频率分布直方图如图:
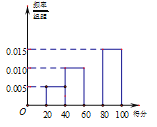
(1)依据统计结果的部分频率分布直方图,求班级卫生量化打分检查得分的中位数;
(2)学校用分层抽样的方法,从评定等级为“良”、“中”的班级中抽取6个班级,再从这6个班级中随机抽取2个班级进行抽样复核,求所抽取的2个班级获得的奖励小红旗面数和不少于3的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有关部门在某公交站点随机抽取了100名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,乘车等待时间不超过40分钟),将数据按![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() 分组,绘制成如图所示的频率分布直方图.
分组,绘制成如图所示的频率分布直方图.
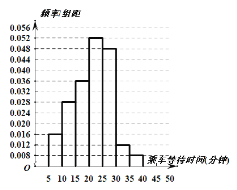
假设乘客乘车等待时间相互独立.
(1)求抽取的100名乘客乘车等待时间的中位数(保留一位小数);
(2)现从该车站等车的乘客中随机抽取4人,记等车时间在![]() 的人数为
的人数为![]() ,用频率估计概率,求随机变量
,用频率估计概率,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,各项为正的等比数列
为等差数列,各项为正的等比数列![]() 的前n项和为
的前n项和为![]() , ,且
, ,且![]() ,
,![]() ,.在①
,.在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件解答,则按选择第一个解答计分).
这三个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件解答,则按选择第一个解答计分).
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点.
两点.
(1)求过![]() 、
、![]() 、
、![]() 三点的圆
三点的圆![]() 的方程;
的方程;
(2)若![]() 为坐标原点,直线
为坐标原点,直线![]() 与椭圆
与椭圆![]() 和(1)中的圆
和(1)中的圆![]() 分别相切于点
分别相切于点![]() 和点
和点![]() (
(![]() 、
、![]() 不重合),求直线
不重合),求直线![]() 与直线
与直线![]() 的斜率之积.
的斜率之积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com