
【题目】已知函数![]() 与
与![]() 的图象在它们的交点
的图象在它们的交点![]() 处具有相同的切线.
处具有相同的切线.
(1)求![]() 的解析式;
的解析式;
(2)若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)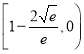
【解析】
(1)求得两个函数的导数,由公切线的斜率相同可得![]() 的方程;将切点代入两个函数,可得
的方程;将切点代入两个函数,可得![]() 的方程;联立两个方程即可求得
的方程;联立两个方程即可求得![]() 的值,进而得
的值,进而得![]() 的解析式;
的解析式;
(2)将![]() 的解析式代入并求得
的解析式代入并求得![]() ,由极值点定义可知
,由极值点定义可知![]() ,
,![]() 是方程
是方程![]() 的两个不等实根,由韦达定理表示出
的两个不等实根,由韦达定理表示出![]() ,结合
,结合![]() 可得
可得![]() .代入
.代入![]() 中化简,分离参数并构造函数
中化简,分离参数并构造函数![]() ,求得
,求得![]() 并令
并令![]() 求得极值点,由极值点两侧符号判断单调性,并求得最小值,代入端点值求得最大值,即可求得
求得极值点,由极值点两侧符号判断单调性,并求得最小值,代入端点值求得最大值,即可求得![]() 的取值范围.
的取值范围.
(1)根据题意,函数![]() 与
与![]()
可知![]() ,
,![]() ,
,
两图象在点![]() 处有相同的切线,
处有相同的切线,
所以两个函数切线的斜率相等,即![]() ,化简得
,化简得![]() ,
,
将![]() 代入两个函数可得
代入两个函数可得![]() ,
,
综合上述两式可解得![]() ,
,
所以![]() .
.
(2)函数![]() ,定义域为
,定义域为![]() ,
,
![]() ,
,
因为![]() ,
,![]() 为函数
为函数![]() 的两个极值点,
的两个极值点,
所以![]() ,
,![]() 是方程
是方程![]() 的两个不等实根,
的两个不等实根,
由根与系数的关系知![]() ,
,![]() ,
,![]()
又已知![]() ,所以
,所以![]() ,
,
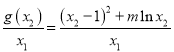 ,
,
将![]() 式代入得
式代入得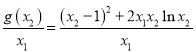
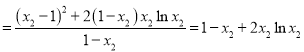 ,
,
令![]() ,
,![]() ,
,
![]() ,令
,令![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递增;
单调递增;
所以 ,
,
![]() ,
,
![]() ,
,
即![]() 的取值范围是
的取值范围是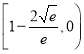 .
.


科目:高中数学 来源: 题型:
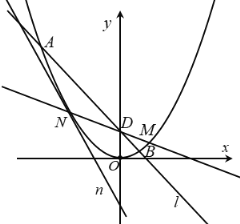
【题目】如图,在平面直角坐标系xOy中,点![]() 在抛物线
在抛物线![]() 上,直线
上,直线![]() 与抛物线C交于A,B两点,且直线OA,OB的斜率之和为
与抛物线C交于A,B两点,且直线OA,OB的斜率之和为![]() .
.
(1)求a和k的值;
(2)若![]() ,设直线
,设直线![]() 与y轴交于D点,延长MD与抛物线C交于点N,抛物线C在点N处的切线为n,记直线n,
与y轴交于D点,延长MD与抛物线C交于点N,抛物线C在点N处的切线为n,记直线n,![]() 与x轴围成的三角形面积为S.求S的最小值.
与x轴围成的三角形面积为S.求S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学对参加“社会实践活动”的全体志愿者进行学分考核,因该批志愿者表现良好,大学决定考核只有合格和优秀两个等次,若某志愿者考核合格,授予![]() 个学分;考核优秀,授予
个学分;考核优秀,授予![]() 个学分,假设该大学志愿者甲、乙、丙考核优秀的概率为
个学分,假设该大学志愿者甲、乙、丙考核优秀的概率为![]() 、
、![]() 、
、![]() .他们考核所得的等次相互独立.
.他们考核所得的等次相互独立.
(1)求在这次考核中,志愿者甲、乙、丙三人中至少一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名志愿者所得学分之和为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
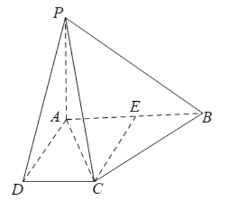
【题目】如图所示,在棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,PA=AD=DC=2,AB=4且AB∥CD,∠BAD=90°.
(1)求证:BC⊥PC;
(2)求PB与平面PAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
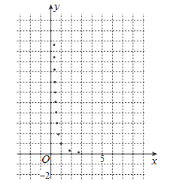
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若旋转的弧度数![]() 与单位时间内煤气输出量
与单位时间内煤气输出量![]() 成正比,那么
成正比,那么![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为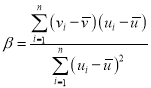 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com