
【题目】已知函数![]() .
.
(1)求![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(2)若过点![]() 存在3条直线与曲线
存在3条直线与曲线![]() 相切,求
相切,求![]() 的取值范围;
的取值范围;
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)求![]() ,令
,令![]() ,求出极值点,极值和区间端点的函数值,即求最大值;
,求出极值点,极值和区间端点的函数值,即求最大值;
(2)设出切点,写出切线方程,把点![]() 的坐标代入切线方程,得
的坐标代入切线方程,得![]() .设
.设![]() ,则“过点
,则“过点![]() 存在3条直线与曲线
存在3条直线与曲线![]() 相切”等价于“
相切”等价于“![]() 有3个不同的零点”.求
有3个不同的零点”.求![]() ,判断
,判断![]() 的单调性,即可求解.
的单调性,即可求解.
(1)由![]() 得
得![]() .
.
令![]() ,得
,得![]() 或
或![]() .
.
因为 ,
,
所以![]() 在区间
在区间![]() 上的最大值为
上的最大值为 .
.
(2)设过点![]() 的直线与曲线
的直线与曲线![]() 相切于点
相切于点![]() ,
,
则![]() ,且切线斜率为
,且切线斜率为![]() ,
,
所以切线方程为![]() ,
,
因此![]() ,
,
整理得![]() .
.
设![]() ,
,
则“过点![]() 存在3条直线与曲线
存在3条直线与曲线![]() 相切”等价于“
相切”等价于“![]() 有3个不同的零点”.
有3个不同的零点”.
![]() .
.
当![]() 变化时,
变化时,![]() 与
与![]() 的变化情况如下:
的变化情况如下:
|
| 0 |
| 1 |
|
| + | 0 | - | 0 | + |
|
|
|
|
|
|
所以,![]() 是
是![]() 的极大值,
的极大值,
![]() 是
是![]() 的极小值.
的极小值.
当![]() ,即
,即![]() 时,
时,
![]() 在区间
在区间![]() 和
和![]() 上分别至多有1个零点,
上分别至多有1个零点,
以![]() 至多有2个零点.
至多有2个零点.
当![]() ,即
,即![]() 时,
时,
![]() 在区间
在区间![]() 和
和![]() 上分别至多有1个零点,
上分别至多有1个零点,
所以![]() 至多有2个零点.
至多有2个零点.
当![]() 且
且![]() ,即
,即![]() 时,
时,
因为![]() ,
,
所以![]() 分别在区间
分别在区间![]() 和
和![]() 上恰有1个零点.
上恰有1个零点.
由于![]() 在区间
在区间![]() 和
和![]() 上单调,
上单调,
所以![]() 分别在区间
分别在区间![]() 和
和![]() 上恰有1个零点.
上恰有1个零点.
综上可知,当过点![]() 存在3条直线与曲线
存在3条直线与曲线![]() 相切时,
相切时,![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,证明函数
时,证明函数![]() 是增函数;
是增函数;
(2)是否存在实数![]() ,使得只有唯一的正数
,使得只有唯一的正数![]() ,当
,当![]() 时恒有:
时恒有:![]() ,若这样的实数
,若这样的实数![]() 存在,试求
存在,试求![]() 、
、![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某仪器经过检验合格才能出厂,初检合格率为![]() :若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为
:若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为![]() .每台仪器各项费用如表:
.每台仪器各项费用如表:
项目 | 生产成本 | 检验费/次 | 调试费 | 出厂价 |
金额(元) | 1000 | 100 | 200 | 3000 |
(Ⅰ)求每台仪器能出厂的概率;
(Ⅱ)求生产一台仪器所获得的利润为1600元的概率(注:利润![]() 出厂价
出厂价![]() 生产成本
生产成本![]() 检验费
检验费![]() 调试费);
调试费);
(Ⅲ)假设每台仪器是否合格相互独立,记![]() 为生产两台仪器所获得的利润,求
为生产两台仪器所获得的利润,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
: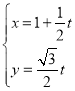 (
(![]() 为参数),曲线
为参数),曲线![]() :
:![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点P是曲线
,设点P是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点 .
.
(1)求![]() 的方程;
的方程;
(2)是否存在直线![]() 与
与![]() 相交于
相交于![]() 两点,且满足:①
两点,且满足:①![]() 与
与![]() (
(![]() 为坐标原点)的斜率之和为2;②直线
为坐标原点)的斜率之和为2;②直线![]() 与圆
与圆![]() 相切,若存在,求出
相切,若存在,求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“干支纪年法”是中国历法上自古以来使用的纪年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”。“天干”以“甲”字开始,“地支”以“子”字开始,两者按干支顺序相配,组成了干支纪年法,其相配顺序为:甲子、乙丑、丙寅…癸酉,甲戌、乙亥、丙子…癸末,甲申、乙酉、丙戌…癸巳,…,共得到![]() 个组成,周而复始,循环记录。2014年是“干支纪年法”中的甲午年,那么2020年是“干支纪年法”中的()
个组成,周而复始,循环记录。2014年是“干支纪年法”中的甲午年,那么2020年是“干支纪年法”中的()
A. 己亥年 B. 戊戌年 C. 庚子年 D. 辛丑年
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com