练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】求下列函数的零点的个数：

    （1）；

    （2）.

    【答案】（1）1个；（2）1个

    【解析】

    （1）首先利用零点存在性定理判断函数在（0，1）内有零点，再结合函数为单调递增函数即可求解；同时也可以函数的零点，转化为与的图象的交点，利用交点个数也可求解.

    （2）首先利用零点存在性定理判断函数在区间内有零点，

    再结合函数为单调递增函数即可求解；也可将函数的零点，转化为与的图象的交点，利用函数图像交点个数也可求解.

    解：方法一：（1）∵，，∴，

    ∴在（0，1）内有零点.又∵在R上是单调增函数，

    ∴在R上有且只有一个零点.

    （2）∵，，

    函数在区间内有零点，

    又∵在R上是单调增函数，

    ∴在R上有且只有一个零点.

    方法二： （1）函数的零点，即方程的根，

    也即的根，令，，

    在同一坐标系中作出两个函数的大致图象，如图，

    由图知与的图象有且只有一个交点，

    即函数只有一个零点.

    （2）函数的零点，

    即方程的根，也即的根.

    令，，在同一坐标系中作出两个函数的大致图象，如图

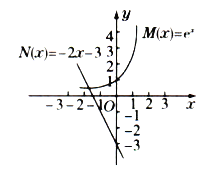
    由图知与的图象有且只有一个交点，

    即函数只有一个零点.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某学校需要从甲、乙两名学生中选一人参加数学竞赛，抽取了近期两人次数学考试的成绩，统计结果如下表：

    第一次

    第二次

    第三次

    第四次

    第五次

    甲的成绩(分)

    乙的成绩(分)

    (1)若从甲、乙两人中选出一人参加数学竞赛，你认为选谁合适?请说明理由.

    (2)若数学竞赛分初赛和复赛，在初赛中有两种答题方案：

    方案一：每人从道备选题中任意抽出道，若答对，则可参加复赛，否则被淘汰.

    方案二：每人从道备选题中任意抽出道，若至少答对其中道，则可参加复赛，否则被润汰.

    已知学生甲、乙都只会道备选题中的道，那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的通项公式为an＝则数列{an}中的最大项为(　　)

    A.B.

    C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P-ABCD中，底面ABCD为正方形，平面PAD⊥平面ABCD，点M在线段PB上，PD//平面MAC,PA=PD=,AB=4.

    (1)求证：M为PB的中点；

    (2)求二面角B-PD-A的大小；

    (3)求直线MC与平面BDP所成角的正炫值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响，随机选取名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.试验数据分别列于表和表.统计方法中，同一组数据常用该组区间的中点值作为代表.

    停车距离（米）

    频数

    表

    平均每毫升血液酒精含量毫克

    平均停车距离米

    表

    （1）根据最小二乘法，由表的数据计算关于的回归方程；

    （2）该测试团队认为：驾驶员酒后驾车的平均“停车距离”大于无酒状态下（表）的停车距离平均数的倍，则认定驾驶员是“醉驾”.请根据（1）中的回归方，预测当每毫升血液酒精含量大于多少毫克时为“醉驾”？

    附：回归方程中，，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱ABC﹣A1B1C1中，AA1C1C是边长为4的正方形．平面ABC⊥平面AA1C1C，AB=3，BC=5．

    （Ⅰ）求证：AA1⊥平面ABC；

    （Ⅱ）求证二面角A1﹣BC1﹣B1的余弦值；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响，随机选取名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.试验数据分别列于表和表.统计方法中，同一组数据常用该组区间的中点值作为代表.

    停车距离（米）

    频数

    表

    平均每毫升血液酒精含量毫克

    平均停车距离米

    表

    （1）根据最小二乘法，由表的数据计算关于的回归方程；

    （2）该测试团队认为：驾驶员酒后驾车的平均“停车距离”大于无酒状态下（表）的停车距离平均数的倍，则认定驾驶员是“醉驾”.请根据（1）中的回归方程，预测当每毫升血液酒精含量大于多少毫克时为“醉驾”？

    附：回归方程中，，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，若函数有三个不同的零点，则实数的取值范围是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】根据以往的经验，某建筑工程施工期间的降水量（单位： ）对工期的影响如下表：

    根据某气象站的资料，某调查小组抄录了该工程施工地某月前20天的降水量的数据，绘制得到降水量的折线图，如下图所示.

    （1）根据降水量的折线图，分别求该工程施工延误天数的频率；

    （2）以（1）中的频率作为概率，求工期延误天数的分布列及数学期望与方差.

    查看答案和解析>>

    同步练习册答案