
【题目】如图1,2,在Rt△ABC中,AB=BC=4,点E在线段AB上,过点E作交AC于点F,将△AEF沿EF折起到△PEF的位置(点A与P重合),使得∠PEB=60°. 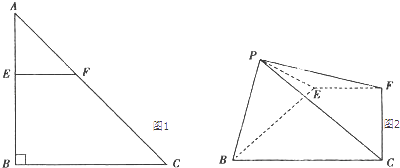
(1)求证:EF⊥PB;
(2)试问:当点E在何处时,四棱锥P﹣EFCB的侧面的面积最大?并求此时四棱锥P﹣EFCB的体积及直线PC与平面EFCB所成角的正切值.
【答案】
(1)证明:∵EF∥BC且BC⊥AB,
∴EF⊥AB,即EF⊥BE,EF⊥PE.又BE∩PE=E,
∴EF⊥平面PBE,又PB平面PBE,
∴EF⊥PB
(2)证明:解:设BE=x,PE=y,则x+y=4.
∴ ![]() .
.
当且仅当x=y=2时,S△PEB的面积最大,此时,BE=PE=2.
由(1)知EF⊥平面PBE,
∵EF平面EFCB,∴平面EFCB⊥平面PBE.
在平面PBE中,作PO⊥BE于O,则PO⊥平面EFCB.
即PO为四棱锥P﹣EFCB的高.
又 ![]() .
.
∴ ![]()
∵ ![]() ,
,
∴BO=1,在Rt△OBC中, ![]() .
.
∵PO⊥平面EFCB,∴∠PCO就是PC与平面EFCB所成角.
∴ ![]() ,
,
故直线PC与平面EFCB所成角的正切值为 ![]()
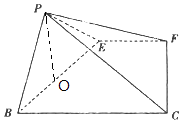
【解析】(1)推导出EF⊥AB,EF⊥BE,EF⊥PE,由此能证明EF⊥PB. (2)设BE=x,PE=y,则x+y=4,当且仅当x=y=2时,S△PEB的面积最大,此时,BE=PE=2.EF⊥平面PBE,从而平面EFCB⊥平面PBE.作PO⊥BE于O,则PO为四棱锥P﹣EFCB的高,∠PCO就是PC与平面EFCB所成角.由此能求出结果.
【考点精析】掌握空间中直线与直线之间的位置关系和空间角的异面直线所成的角是解答本题的根本,需要知道相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则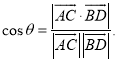 .
.


科目:高中数学 来源: 题型:
【题目】在测试中,客观题难题的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度, ![]() 为答对该题的人数,
为答对该题的人数, ![]() 为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:

测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如下表所示(“√”表示答对,“×”表示答错):
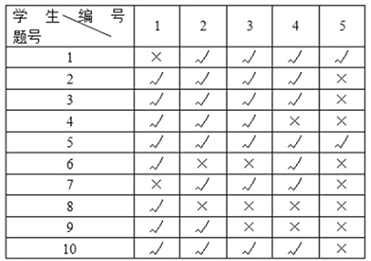
(1)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表,并估计这120名学生中第5题的实测答对人数;

(2)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率;
(3)定义统计量![]() ,其中
,其中![]() 为第
为第![]() 题的实测难度,
题的实测难度, ![]() 为第
为第![]() 题的预估难度(
题的预估难度(![]() ).规定:若
).规定:若![]() ,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若{ ![]() 、
、 ![]() 、
、 ![]() }为空间的一组基底,则下列各项中,能构成基底的一组向量是( )
}为空间的一组基底,则下列各项中,能构成基底的一组向量是( )
A.![]() ,
, ![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]()
B.![]() ,
, ![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]()
C.![]() ,
, ![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]()
D.![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]() ,
, ![]() +2
+2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=2,BC= ![]() ,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( )
,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,双曲线C: ![]() =1(a>0,b>0)的左焦点为F(﹣c,0)(c>0),以OF为直径的圆交双曲线C的渐近线于A,B,O三点,且(
=1(a>0,b>0)的左焦点为F(﹣c,0)(c>0),以OF为直径的圆交双曲线C的渐近线于A,B,O三点,且( ![]() +
+ ![]() )
) ![]() =0,若关于x的方程ax2+bx﹣c=0的两个实数根分别为x1和x2 , 则以|x1|,|x2|,2为边长的三角形的形状是( )
=0,若关于x的方程ax2+bx﹣c=0的两个实数根分别为x1和x2 , 则以|x1|,|x2|,2为边长的三角形的形状是( )
A.钝角三角形
B.直角三角形
C.锐角三角形
D.等腰直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com