
分数段 | 午休的考生成绩 | 不午休的考生成绩 |
29~40 | 23 | 17 |
41~50 | 47 | 51 |
51~59 | 30 | 67 |
60~70 | 21 | 15 |
71~80 | 14 | 30 |
81~90 | 31 | 17 |
91~100 | 14 | 3 |
(1)请根据上述表格完成列联表.
| 及格人数 | 不及格人数 | 总计 |
午休 |
|
|
|
不午休 |
|
|
|
总计 |
|
|
|
(2)根据列联表可以得出什么样的结论?对今后的复习有什么指导意义?
思路分析:要正确给出列联表,首先要把表中的数据进行统计,分别计算出午休和不午休时对应的及格及不及格人数,然后填入相应表格即可;根据列联表可以粗略判断出变量之间是否有关系.
解:(1)根据表中数据可以得出列联表中的数据如下:
| 及格人数 | 不及格人数 | 总计 |
午休 | 80 | 100 | 180 |
不午休 | 65 | 135 | 200 |
总计 | 145 | 235 | 380 |
(2)计算可知,午休的考生及格率为P1=![]() ,不午休的考生及格率为P2=
,不午休的考生及格率为P2=![]() ,显然P1>P2.
,显然P1>P2.
因此,可以粗略判断午休对考生考试及格有关系,并且午休的及格率高,所以,在以后的复习中考生应尽量适当午休,以保持最佳的学习状态.
绿色通道:列联表是对数据的一种简单统计,也是对数据的一种整理,在列联表中可以看出每种变量对应的数据的频数和总计数量,进而可以计算对应变量的频率,再用频率代替概率,可以粗略估计两个分类变量是否有关系.
黑色陷阱:列联表是对相应数据频数的统计,在判断两个分类变量是否有关系时不是看频数的大小,而是要结合列联表计算出频率,再对变量的关系进行估计,否则可能得出错误的结论;根据列联表进行的判断只是对两个变量之间的粗略估计,有时候可能是错误的,所以,还要进一步判断,否则也可能得出错误的结论.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
| 成绩 | 2a=6,
|
a=3,c=
|
|
|
△=144k2-12(1+3k2)>0, | |||||||||||||||||||||
| 频数 | 4 | 20 | 15 | 10 | 1 |
| 成绩 | k2>
|
A(x1,y1),B(x2,y2) | x1+x2=
|
y1+y2=k(x1+x2)-4=k•
|
E(
| ||||||||||||||
| 频数 | 1 | 11 | 23 | 13 | 2 |
| 成绩小于100分 | 成绩不小于100分 | 合计 | |||||||
| 甲班 |
|
26 | 50 | ||||||
| 乙班 | 12 | k=±1 | 50 | ||||||
| 合计 | 36 | 64 | 100 |
| x-y-2=0或x+y+2=0. | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | ||
a=
|
2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5.
为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5.查看答案和解析>>
科目:高中数学 来源: 题型:
| 分数段 | [29~40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 午休考生 人数 |
23 | 47 | 30 | 21 | 14 | 31 | 14 |
| 不午休考 生人数 |
17 | 51 | 67 | 15 | 30 | 17 | 3 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
| 及格人数 | 不及格人数 | 总计 | |
| 午休 | |||
| 不午休 | |||
| 总计 |
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 北师大课标高二版(选修1-2) 2009-2010学年 第28期 总第184期 北师大课标 题型:044
在某次测试中,卷面满分为100分,60分为及格.为了调查午休对本次测试前两个月的复习效果是否有影响,特对复习中进行午休和不进行午休的考生进行了测试成绩的统计,数据如下:
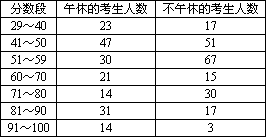
(1)请根据上述表格完成下表中的列联表:

(2)根据列联表可以得出什么样的结论?对今后的复习有什么指导意义?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com