
【题目】设![]() 和
和![]() 是双曲线
是双曲线![]() 上的两点,线段
上的两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 不经过坐标原点
不经过坐标原点![]() .
.
(1)若直线![]() 和直线
和直线![]() 的斜率都存在且分别为
的斜率都存在且分别为![]() 和
和![]() ,求证:
,求证:![]() ;
;
(2)若双曲线的焦点分别为![]() 、
、![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求由四点
,求由四点![]() 、
、![]() 、
、![]() 、
、![]() 所围成四边形
所围成四边形![]() 的面积.
的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)法一:设不经过点![]() 的直线
的直线![]() 方程为
方程为![]() ,与双曲线方程联立,利用中点坐标表示
,与双曲线方程联立,利用中点坐标表示![]() ,再求
,再求![]() ;法二:利用点差法表示
;法二:利用点差法表示![]() ;
;
(2)先由已知求得双曲线方程和直线![]() 的方程,由条件表示四边形的面积
的方程,由条件表示四边形的面积![]() ;令解,利用
;令解,利用![]() 的中点是
的中点是![]() ,直接求点
,直接求点![]() 的坐标,再表示四边形的面积
的坐标,再表示四边形的面积![]() .
.
(1)证明:法1:设不经过点![]() 的直线
的直线![]() 方程为
方程为![]() ,代入双曲线
,代入双曲线![]() 方程得:
方程得:![]() .
.
设![]() 坐标为
坐标为![]() ,
,![]() 坐标为
坐标为![]() ,中点坐标为
,中点坐标为![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,所以,
,所以,![]() ,
,![]() .
.
法2:设![]() 、
、![]() ,中点
,中点![]() ,则
,则![]() ,
,![]() 且
且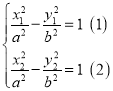 ,
,
(1)﹣(2)得:![]() .
.
因为,直线![]() 和直线
和直线![]() 的斜率都存在,所以
的斜率都存在,所以![]() ,
,
等式两边同除以![]() ,得:
,得:![]() ,即
,即![]() .
.
(2)由已知得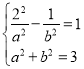 ,求得双曲线方程为
,求得双曲线方程为![]() ,直线
,直线![]() 斜率为
斜率为![]() ,
,
直线![]() 方程为
方程为![]() ,代入双曲线方程可解得
,代入双曲线方程可解得![]() ,中点
,中点![]() 坐标为
坐标为![]() .
.
面积![]() .
.
另解:线段![]() 中点
中点![]() 在直线
在直线![]() 上.所以由中点
上.所以由中点![]() ,可得点
,可得点![]() 的坐标为
的坐标为![]() ,代入双曲线方程可得
,代入双曲线方程可得![]() ,即
,即![]() ,解得
,解得![]() (
(![]() ),所以
),所以![]() .面积
.面积![]() .
.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】中华文化博大精深,源远流长,每年都有大批外国游客入境观光旅游或者学习等,下面是![]() 年至
年至![]() 年三个不同年龄段外国入境游客数量的柱状图:
年三个不同年龄段外国入境游客数量的柱状图:
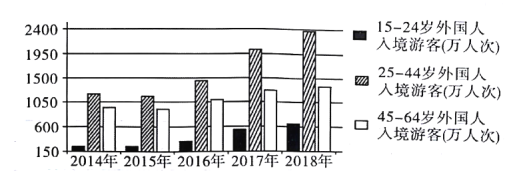
下面说法错误的是:( )
A.![]() 年至
年至![]() 年外国入境游客中,
年外国入境游客中,![]() 岁年龄段人数明显较多
岁年龄段人数明显较多
B.![]() 年以来,三个年龄段的外国入境游客数量都在逐年增加
年以来,三个年龄段的外国入境游客数量都在逐年增加
C.![]() 年以来,
年以来,![]() 岁外国入境游客增加数量大于
岁外国入境游客增加数量大于![]() 岁外国入境游客增加数量
岁外国入境游客增加数量
D.![]() 年,
年,![]() 岁外国入境游客增长率大于
岁外国入境游客增长率大于![]() 岁外国入境游客增长率
岁外国入境游客增长率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为整数,其前n项和为Sn.规定:若数列{an}满足前r项依次成公差为1的等差数列,从第r﹣1项起往后依次成公比为2的等比数列,则称数列{an}为“r关联数列”.
(1)若数列{an}为“6关联数列”,求数列{an}的通项公式;
(2)在(1)的条件下,求出Sn,并证明:对任意n∈N*,anSn≥a6S6;
(3)已知数列{an}为“r关联数列”,且a1=﹣10,是否存在正整数k,m(m>k),使得a1+a2+…+ak﹣1+ak=a1+a2+…+am﹣1+am?若存在,求出所有的k,m值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检测某种零件的一条生产线的生产过程,从生产线上随机抽取一批零件,根据其尺寸的数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 组,得到如图所示的频率分布直方图.若尺寸落在区间
组,得到如图所示的频率分布直方图.若尺寸落在区间![]() 之外,则认为该零件属“不合格”的零件,其中
之外,则认为该零件属“不合格”的零件,其中![]() ,
,![]() 分别为样本平均和样本标准差,计算可得
分别为样本平均和样本标准差,计算可得![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
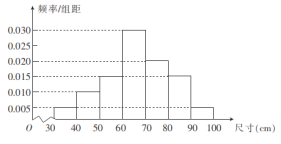
(1)若一个零件的尺寸是![]() ,试判断该零件是否属于“不合格”的零件;
,试判断该零件是否属于“不合格”的零件;
(2)工厂利用分层抽样的方法从样本的前![]() 组中抽出
组中抽出![]() 个零件,标上记号,并从这
个零件,标上记号,并从这![]() 个零件中再抽取
个零件中再抽取![]() 个,求再次抽取的
个,求再次抽取的![]() 个零件中恰有
个零件中恰有![]() 个尺寸小于
个尺寸小于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 和
和![]() 是双曲线
是双曲线![]() 上的两点,线段
上的两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 不经过坐标原点
不经过坐标原点![]() .
.
(1)若直线![]() 和直线
和直线![]() 的斜率都存在且分别为
的斜率都存在且分别为![]() 和
和![]() ,求证:
,求证:![]() ;
;
(2)若双曲线的焦点分别为![]() 、
、![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求由四点
,求由四点![]() 、
、![]() 、
、![]() 、
、![]() 所围成四边形
所围成四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在实数集![]() 上的偶函数
上的偶函数![]() 和奇函数
和奇函数![]() 满足
满足![]() .
.
(1)求![]() 与
与![]() 的解析式;
的解析式;
(2)求证:![]() 在区间
在区间![]() 上单调递增;并求
上单调递增;并求![]() 在区间
在区间![]() 的反函数;
的反函数;
(3)设![]() (其中
(其中![]() 为常数),若
为常数),若![]() 对于
对于![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两队参加听歌猜歌名游戏,每队![]() 人.随机播放一首歌曲, 参赛者开始抢答,每人只有一次抢答机会,答对者为本队赢得一分,答错得零分, 假设甲队中每人答对的概率均为
人.随机播放一首歌曲, 参赛者开始抢答,每人只有一次抢答机会,答对者为本队赢得一分,答错得零分, 假设甲队中每人答对的概率均为![]() ,乙队中
,乙队中![]() 人答对的概率分别为
人答对的概率分别为![]() ,且各人回答正确与否相互之间没有影响.
,且各人回答正确与否相互之间没有影响.
(1)若比赛前随机从两队的![]() 个选手中抽取两名选手进行示范,求抽到的两名选手在同一个队的概率;
个选手中抽取两名选手进行示范,求抽到的两名选手在同一个队的概率;
(2)用![]() 表示甲队的总得分,求随机变量
表示甲队的总得分,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(3)求两队得分之和大于4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的函数,满足
上的函数,满足 .
.
(1)证明:2是函数![]() 的周期;
的周期;
(2)当![]() 时,
时,![]() ,求
,求![]() 在
在![]() 时的解析式,并写出
时的解析式,并写出![]() 在
在![]() (
(![]() )时的解析式;
)时的解析式;
(3)对于(2)中的函数![]() ,若关于x的方程
,若关于x的方程![]() 恰好有20个解,求实数a的取值范围.
恰好有20个解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某年数学竞赛请自以为来自X星球的选手参加填空题比赛,共10道题目,这位选手做题有一个古怪的习惯:先从最后一题(第10题)开始往前看,凡是遇到会的题就作答,遇到不会的题目先跳过(允许跳过所有的题目),一直看到第1题;然后从第1题开始往后看,凡是遇到先前未答的题目就随便写个答案,遇到先前已答的题目则跳过(例如,他可以按照9,8,7,4,3,2,1,5,6,10的次序答题),这样所有的题目均有作答,设这位选手可能的答题次序有n种,则n的值为( )
A.512B.511C.1024D.1023
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com