
【题目】已知函数f(x)=|x-3|-|x+1|.
(1)求f(x)的值域;
(2)解不等式:f(x)>0;
(3)若直线y=a与f(x)的图像无交点,求实数a的取值范围.
【答案】(1) [-4,4] (2) (-∞,1) (3) a∈(-∞,-4)∪(4,+∞)
【解析】
(1)首先将函数的解析式写成分段函数的形式,然后求解其值域即可;
(2)结合函数的解析式零点分段求解不等式的解集即可;
(3)首先绘制函数f(x)的图像,然后数形结合即可确定实数a的取值范围.
若x≤-1,则x-3<0,x+1≤0,
f(x)=-(x-3)+(x+1)=4;
若-1<x≤3,则x-3≤0,x+1>0,
f(x)=-(x-3)-(x+1)=-2x+2;
若x>3,则x-3>0,x+1>0,
f(x)=(x-3)-(x+1)=-4.
∴f(x)=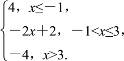
(1)-1<x≤3时,-4≤-2x+2<4.
∴f(x)的值域为[-4,4)∪{4}∪{-4}=[-4,4].
(2)f(x)>0,即![]() ①
①
或![]() ②
②
或![]() ③
③
解①得x≤-1,解②得-1<x<1,解③得x∈.
∴f(x)>0的解集为(-∞,-1]∪(-1,1)∪=(-∞,1).
(3)f(x)的图像如下:
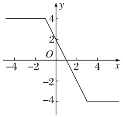
由图可知,当a∈(-∞,-4)∪(4,+∞)时,直线y=a与f(x)的图像无交点.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】已知右焦点为![]() 的椭圆
的椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点.
对称的图形过坐标原点.
![]() 是椭圆
是椭圆![]() 的左顶点,斜率为
的左顶点,斜率为![]() 的直线交
的直线交![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() 在
在![]() 上,
上,![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的面积;
的面积;
(Ⅱ)当![]() 时,证明:
时,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学有着辉煌和灿烂的历史,成书于公元一世纪的数学著作《九章算术》中有一道关于数列的题目:“今有良马与驽马发长安至齐。齐去长安三千里。良马初日行一百九十三里,日增十三里。驽马初日行九十七里,日减半里。良马先至齐,复还迎驽马。问几何日相逢及各行几何?”根据你所学数列知识和数学运算技巧计算两马相逢时是在出发后的第_______天(写出整数即可).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求函数![]() 的极值
的极值
(2)定义:若函数![]() 在区间
在区间![]()
![]() 上的取值范围为
上的取值范围为![]() ,则称区间
,则称区间![]() 为函数
为函数![]() 的“美丽区间”.试问函数
的“美丽区间”.试问函数![]() 在
在![]() 上是否存在“美丽区间”?若存在,求出所有符合条件的“美丽区间”;若不存在,请说明理由
上是否存在“美丽区间”?若存在,求出所有符合条件的“美丽区间”;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)用分段函数的形式表示函数f(x);
(2)在平面直角坐标系中画出函数f(x)的图象;

(3)在同一平面直角坐标系中,再画出函数g(x)=![]() (x>0)的图象(不用列表),观察图象直接写出当x>0时,不等式f(x)>
(x>0)的图象(不用列表),观察图象直接写出当x>0时,不等式f(x)> ![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】被嘉定著名学者钱大昕赞誉为“国朝算学第一”的清朝数学家梅文鼎曾创造出一类“方灯体”,“灯者立方去其八角也”,如图所示,在棱长为![]() 的正方体
的正方体![]() 中,点
中,点![]() 为棱上的四等分点.
为棱上的四等分点.

(1)求该方灯体的体积;
(2)求直线![]() 和
和![]() 的所成角;
的所成角;
(3)求直线![]() 和平面
和平面![]() 的所成角.
的所成角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂拟制造一个如图所示的容积为36π立方米的有盖圆锥形容器.
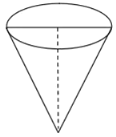
(1)若该容器的底面半径为6米,求该容器的表面积;
(2)当容器的高为多少米时,制造该容器的侧面用料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() 是定义域为
是定义域为![]() 的奇函数.
的奇函数.
(1)确定![]() 的值;
的值;
(2)若![]() ,函数
,函数![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(3)若![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com